Уравнение Шрёдингера – основное уравнение нерелятивистской квантовой механики. Уравнение Шрёдингера для стационарных состояний. §217. Общее уравнение Шредингера. Уравнение Шредингера для стационарных состояний
где – оператор Гамильтона – аналог классической функции Гамильтона
![]()
в которой и заменены операторами импульса x , y , z и координаты , , :
х → = х, y → = y, z → = z,
| (4.2) |
Уравнение ШредингераЗависящее от времени уравнение Шредингера: где – гамильтониан системы. Разделение переменных. Запишем Ψ(,t) = ψ()θ(t), где ψ является функцией координат, а θ – функция времени. Если не зависит от времени, тогда уравнение ψ = iћψ принимает вид θψ = iћψθ или Левая часть является функцией только координат, а правая не зависит от переменной x. Поэтому обе части последнего уравнения должны быть равны одной и той же постоянной, которую обозначим E
Следовательно, θ(t) = exp(−iEt/ћ), ψ() = Eψ() и Ψ(,t) = ψ()exp(−iEt/ћ). Уравнение ψ() = Eψ() называют стационарным уравнением Шредингера. Для одномерной системы с массой m в поле с потенциалом U(x) оно принимает вид:
Для трехмерной системы с массой m в поле с потенциалом U(): −(ћ 2 /2m)Δψ() + U()ψ() = Eψ(), где Δ – лапласиан. |
Так как уравнение Шредингера является линейным уравнением первого порядка по времени, то с его помощью по заданному значению волновой функции Ψ(x, y, z, 0) в момент времени t = 0 можно найти её значение в произвольный момент времени t − Ψ(x, y, z, t).
Уравнение Шредингера для стационарного состояния, когда потенциальная энергия частицы не зависит от времени, имеет вид
| ψ() = Eψ(). | (4.3) |
Это уравнение называют стационарным уравнением Шредингера.
Так как в стационарном состоянии
| Ψ(,t) = ψ()exp(−iEt/ћ) | (4.4) |
и вероятность найти частицу в момент t в точке x, y, z пропорциональна |Ψ(,t)|, то она ~ |ψ(x,y,z)| 2 , т.е. не зависит от времени. Аналогично, вероятность обнаружить значение физической величины, характеризующей систему, также не изменяется со временем, поскольку выражается через квадрат модуля волновой функции.
4.2 . Частица в одномерной прямоугольной яме с бесконечными стенками
Потенциальная энергия U(x) в прямоугольной яме удовлетворяет следующим условиям:
Частица находится в области 0 ≤ x ≤ L. Вне этой области ψ(x) = 0. Уравнение Шредингера для частицы, находящейся в области 0 ≤ x ≤ L
где k = (2mE/ћ 2) 1/2 . Из граничных условий ψ(0) = 0, ψ(L) = 0 и условий непрерывности волновой функции следует
Частица может находиться в
каком-то одном из множества дискретных состояний, доступных для неё.
Каждому значению энергии E n соответствует
волновая функция ψ n (x), которая с учетом
условия нормировки
![]()
имеет вид
|
|
(4.10) |
В отличие от классической, квантовая частица в прямоугольной яме не может
иметь энергию
E < ћ 2 π 2 /(2mL 2).
Состояния частицы ψ n в
одномерном поле бесконечной потенциальной ямы полностью описывается с помощью
одного квантового числа n. Спектр энергий дискретный.

Рис. 4.2. Уровни энергии и волновые функции частицы Ψ в бесконечной прямоугольной яме. Квадрат модуля волновой функции |Ψ| 2 определяет вероятность нахождения частицы в различных точках потенциальной ямы.
4.3 . Гармонический осциллятор
Положение уровней частицы в потенциальной яме зависит от вида потенциальной ямы. В одномерной потенциальной яме гармонического осциллятора потенциальная энергия имеет вид
Допустимые значения полной энергии определяются формулой
| E n = ћω 0 (n + 1/2), n = 0, 1, 2, | (4.13) |
В отличие от бесконечной прямоугольной ямы, спектр уровней гармонического
осциллятора эквидистантный.
С увеличением массы частицы или размеров области ее локализации квантовое
описание частицы переходит в классическое.
4.4 . Частица в поле с центральной симметрией
В сферических координатах стационарное уравнение Шредингера для частицы в центральном потенциале U(r) имеет вид
где радиальная функция R nl (r) и угловая функция Y lm (θ,φ), называемая сферической, удовлетворяют уравнениям
| 2 Y lm (θ,φ) = ћ 2 l (l +1)Y lm (θ,φ) | (4.16) |
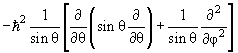 Y lm (θ,φ)
= ћ 2 l
(l
+1)Y lm (θ,φ) Y lm (θ,φ)
= ћ 2 l
(l
+1)Y lm (θ,φ) |
(4.17) |
Уравнение (4.16) определяет возможные собственные значения
l
и собственные функции Y lm (θ,φ) оператора
квадрата момента 2 .
Уравнение (4.17) определяет собственные значения энергии Е и радиальные
собственные функции R nl (r),
от которых зависит энергия системы (рис. 4.3).
Схема уровней (последовательность и абсолютные значения энергий) зависит от
радиальной функции R nl (r),
которая в свою очередь определяется потенциалом U(r),
в котором находится частица.
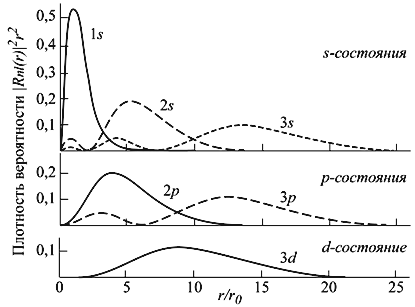
Рис. 4.3. Радиальное распределение вероятности нахождения электрона в
кулоновском поле протона (атом водорода). Расстояния даны в боровских радиусах
r 0 = ћ 2 /m e e 2 ≈
0.529·10 8 cм.
4.5 . Орбитальный момент количества движения
Собственные значения L 2 и L z являются решением уравнений
2 Y lm (θ,φ) = L 2 Y lm (θ,φ) и z Y lm (θ,φ) = L z Y lm (θ,φ).
Они имеют следующие дискретные значения
L 2 =
ћ 2 l(l
+ 1), где l = 0, 1, 2, 3, …,
L z =
ћm,
где m = 0, ± 1,
± 2, ± 3,…,
± l.
Для характеристики состояний с различными значениями орбитального момента l обычно используют следующие обозначения:
Спектроскопические названия орбитальных моментов l
| l = 0 | s-состояние |
| l = 1 | p-состояние |
| l = 2 | d-состояние |
| l = 3 | f-состояние |
| l = 4 | g-состояние |
| l = 5 | h-состояние |
| и. т. д. |
Состоянию с l = 0 отвечает сферически симметричная
волновая функция. В тех случаях, когда l ≠ 0
волновая функция не имеет сферической симметрии. Симметрия волновой функции
определяется симметрией сферических функций Y lm (θ,φ).
Имеет место интересное квантовое явление, когда решение сферически симметричной
задачи (потенциал описывает сферически симметричную систему) приводит к
состояниям, не обладающим сферической симметрией. Таким образом, симметрия
уравнений не обязательно должна отражаться в симметрии каждого отдельно взятого
решения этих уравнений, а лишь во всей совокупности
этих решений.
Для частицы, находящейся в сферически симметричном потенциале, величина
орбитального момента количества движения L:
| (4.18) |
Обычно, для упрощения, когда говорят о величине орбитального момента количества движения, называют этой величиной квантовое число l, имея в виду, что между l и L имеется однозначная связь (4.18).
Так как величина l может принимать только целочисленные значения 0, 1, 2, 3,…, то и орбитальный момент количества движения L квантуется. Например, для частицы с l = 2 момент количества движения
=
= 6.58·10 -22 √6
МэВ·сек ≈ 2.6·10 - 34
Дж·сек.
Пространственное квантование
. Орбитальный момент количества движения является
векторной величиной. Так как величина орбитального момента количества движения
квантуется, то и направление
по
отношению к выделенному направлению z, например, к
внешнему магнитному полю, также квантуется и принимает дискретные значения
Lz =
ћm,
где m изменяется от +l до –l,
т. е. имеет 2l + 1 значений. Например, при
l = 2 величина m принимает
значения +2, +1, 0, -1, -2 (см. рис. 4.4). Вместе с тем энергия системы не
зависит от m, т. е. от направления вектора
,
что является очевидным следствием сферической симметрии системы.
Состояние частицы, находящейся в сферически симметричном поле, полностью
описывается тремя квантовыми числами: n,
l и m.
Появление квантовых чисел связано со свойствами симметрии системы. Характер
этой симметрии определяет возможные значения квантовых чисел. Очевидно, что
система, описываемая функцией e im φ , примет прежнее
значение только тогда, когда азимутальный угол φ в результате поворота вокруг
оси z примет прежнее значение φ. Этому условию функция
e im φ удовлетворяет только в случае, когда величина
mφ кратна 2π. Т.е. величина m
должна иметь целые значения. Так как необходимо учитывать вращение в двух
противоположных направлениях и отсутствие вращения, единственно возможными
значениями оказываются m = 0, ±1, ±2, … .
4.6 . Спин
Спин − собственный момент количества движения частицы. Между значением вектора спина и квантовым числом спина s выполняется такое же соотношение, как между величиной значением вектора орбитального момента и орбитальным квантовым числом l:
| 2 = ћ 2 s(s + 1) | (4.19) |
В отличие от орбитального квантового числа l,
которое может быть лишь целым числом или нулем, спиновое квантовое число
s (в дальнейшем просто спин) может быть как целым
(включая нуль), так и полуцелым, т. е. s = 0, 1/2, 1, 3/2, 2, 5/2,
… , но при этом для каждой элементарной частицы спин может принимать
единственное присущее этому типу частиц значение
. Так, спины π-мезонов и К-мезонов
равны 0. Спины электрона, протона, нейтрино, кварков и их античастиц равны 1/2.
Спин фотона равен 1. Бозоны составляют класс частиц с целым значением спина,
спин фермионов имеет полуцелое значение. Спин частицы невозможно изменить, также
как её заряд или массу. Это её неизменная квантовая характеристика.
Как и в случае других квантовых векторов, проекция вектора спина
на
любое фиксированное направление в пространстве (например, на ось
z) может принимать 2s + 1
значение:
s z ћ = ±sћ, ±(s − 1)ћ, ±(s − 2)ћ,..., ±1/2ћ или 0.
Число s z − это квантовое число проекции спина. Максимальная величина s z совпадает с s. Так как спин электрона равен 1/2, то проекция этого спина может принимать лишь два значения s z = ±1/2. Если проекция +1/2, то говорят, что спин направлен вверх, если проекция -1/2, то говорят, что спин направлен вниз.
4.7 . Полный момент количества движения
Полный момент количества движения частицы или системы частиц является векторной суммой орбитального и спинового моментов количества движения.
Квадрат полного момента имеет значение:
2 = ћ 2 j(j + 1).
Квантовое число полного момента j, соответствующее сумме двух векторов и , может принимать ряд дискретных значений, отличающихся на 1:
j = l + s, l + s −1,..., |l − s|
Проекция на выделенную ось J z также принимает дискретные значения:
J z = ћj z ; = -j, -j + 1,..., j − 1, j.
Число значений проекции J z равно 2j + 1. Если для и определены единственные значения проекций на ось z l z и s z , то j z также определена однозначно: j z = l z + s z .
4.8 . Квантовые числа
Квантовые числа – это целые или дробные числа, которые определяют все возможные значения физической величины, характеризующей различные квантовые системы – атомы, атомные ядра, кварки и другие частицы.
Таблица квантовых чисел
| n | Радиальное квантовое число. Определяет число узлов волновой функции и энергию системы. n = 1, 2, …, ∞. |
| J, j | Полный угловой момент J и его квантовое число j. Последнее никогда не бывает отрицательным и может быть целым или полуцелым в зависимости от свойств рассматриваемой системы. 2 = ћ 2 j(j + 1). |
| L, l | Орбитальный угловой момент L и его квантовое число l. Интерпретация l такая же, как j, но l может принимать только целые значения, включая нуль: l = 0, 1, 2,…. L 2 = ћ 2 l(l + 1). |
| m | Магнитное квантовое число. Проекция полного или орбитального углового момента на выделенную ось (обычно ось z) равна mћ. Для полного момента m = ±j, ±(j-1), …, ±1/2 или 0. Для орбитального m = ± l, ± (l-1), …, ±1, 0. |
| S, s | Спиновый угловой момент S и его квантовое число s. Оно может быть либо положительным целым (включая нуль), либо полуцелым. s – неизменная характеристика частицы определенного типа. S 2 = ћ 2 s(s + 1). |
| s z | Квантовое число проекции спинового момента частицы на выделенную ось. Эта проекция может принимать значения s z ћ, где s z = ± s, ± (s -1), …, ±1/2 или 0. |
| P или π | Пространственная четность. Характеризует поведение системы при пространственной инверсии → - (зеркальном отражении). Полная четность частицы Р = π(-1) l , где π – её внутренняя четность, а (-1) l – её орбитальная четность. Внутренние четности кварков положительные, антикварков - отрицательные. |
| I | Изоспин. Характеризует свойство зарядовой инвариантности сильных взаимодействий |
Для обозначения спинового момента часто используют букву J.
Все состояния, в которых может находиться квантовая система, описываются с помощью полного набора квантовых чисел. Так в случае протона в ядре состояние протона описывается с помощью четырех квантовых чисел, соответствующих четырем степеням свободы – трем пространственным координатам и спину. Это
- Радиальное квантовое число n (1, 2, …, ∞),
- Орбитальное квантовое число l (0, 1, 2, …),
- Проекция орбитального момента m (± l, ± (l-1), …, ±1, 0),
- Спин протона s =1/2.
Для описания сферически-симметричных систем в квантовой физике используются различные сферически симметричные потенциалы с различной радиальной зависимостью:
![]()
где U 0 ,
а и R – положительные константы (R
– радиус ядра). Во всех случаях сферически симметричные системы можно
описать с помощью набора квантовых чисел n,
l, j,
j z ,
однако, в зависимости от радиального вида потенциала энергетический спектр
состояний системы будет различным.
Существование сохраняющихся во времени физических величин тесно связано со
свойствами симметрии гамильтониана системы. Например, в случае, если квантовая
система обладает центральной симметрией U = U(r),
то этой системе соответствует сохранение орбитального момента количества
движения l и одной из его проекций
m. При этом из-за сферической симметрии задачи энергия состояний не будет
зависеть от величины m, т. е. состояния будут
вырожденными по m.
Наряду с пространственными симметриями, связанными с непрерывными
преобразованиями, в квантовой физике существуют и другие симметрии –
дискретные. Одной из них является зеркальная симметрия волновой функции
относительно инверсии координат (→
-).
Оператору инверсии соответствует квантовое число четность, которое может
принимать два значения +1 и -1 в зависимости от того, сохраняется ли знак
волновой функции при инверсии или меняется на противоположный.
Система тождественных частиц характеризуется еще одной симметрией –
симметрией относительно перестановок тождественных частиц. Эта симметрия
определяется свойствами частиц, образующих систему. Системы частиц с целым
спином (бозонов) описываются симметричными волновыми функциями, системы частиц с полуцелым
спином (фермионов) − антисимметричными волновыми функциями.
§ 217. Общее уравнение Шредингера. Уравнение Шредингера для стационарных состояний
Статистическое толкование волн да Бройля (см. § 216) и соотношение неопределенностей Гейзенберга (см. §215) привели к выводу, что уравнением движения в квантовой механике, описывающим движение микрочастиц в различных силовых полях, должно быть уравнение, из которого бы вытекали наблюдаемые на опыте волновые свойства частиц. Основное уравнение должно быть уравнением относительно волновой функции (х, у, z , t ), так как именно она, или, точнее, величина, определяет вероятность пребывания частицы в момент времени t в объеме dV , т. е. в области с координатами x и x + dx . y и y + dy . zuz + dz . Так как искомое уравнение должно учитывать волновые свойства частиц, то оно должно быть волновым уравнением, подобно уравнению, описывающему электромагнитные волны.
Основное уравнение нерелятивистской квантовой механики сформулировано в 1926 г. Э. Шредингером. Уравнение Шредингера, как и все основные уравнения физики (например, уравнения Ньютона в классической механике и уравнения Максвелла для электромагнитного поля), не выводится, а постулируется. Правильность этого уравнения подтверждается согласием с опытом получаемых с его помощью результатов, что, в свою очередь, придает ему характер закона природы. Уравнение Шредингера имеет вид
 (217.1)
(217.1)
где,
т
-
масса частицы,-
оператор Лапласа ,
,
- мнимая единица, V {х, у, z , t ) - потенциальная функция частицы в силовом поле, в котором она движется, (х, у, z , t ) - искомая волновая функция частицы.
Уравнение (217.1) справедливо
для любой частицы (со спином, равным 0;
см. § 225), движущейся с малой (по сравнению
со скоростью света) скоростью, т. е. со
скоростью
Оно дополняется условиями, накладываемыми
на волновую функцию: 1) волновая
функция должна быть конечной, однозначной
и непрерывной (см. § 216); 2) производные должны
быть непрерывны; 3) функциядолжна
быть
должны
быть непрерывны; 3) функциядолжна
быть
интегрируема; это условие в простейших случаях сводится к условию нормировки вероятностей (216.3).
Чтобы
прийти к уравнению Шредингера, рассмотрим
свободно движущуюся частицу, которой,
согласно идее де Бройля, сопоставляется
плоская волна. Для простоты рассмотрим
одномерный случай. Уравнение плоской
волны, распространяющейся вдоль оси
х,
имеет
вид (см. § 154)
, или в комплексной записи![]() Следовательно,
плоская
Следовательно,
плоская
волна де Бройля имеет вид
![]() (217.2)
(217.2)
(учтено,
что![]() В
квантовой механике показатель экспоненты
берут со знаком минус,
В
квантовой механике показатель экспоненты
берут со знаком минус,
но поскольку физический смысл имеет только, то это (см. (217.2)) несущественно. Тогда
откуда
Используя взаимосвязь
между энергией
Е
и импульсом![]() и
подставляя выражения
и
подставляя выражения
(217.3), получим дифференциальное уравнение

которое совпадает с уравнением (217.1) для случая U =0 (мы рассматривали свободную частицу).
Если частица движется в силовом поле, характеризуемом потенциальной энергией U , то
полная энергия Е складывается из типич еской и потенциальной энергий. Проводя аналогичные
рассуждения и используя
взаимосвязь между
Е
и
р
(для данного
случая![]() придем
придем
° к дифференциальному уравнению, совпадающему с (217.1).
Приведенные рассуждения не должны восприниматься как вывод уравнения Шреди-нгера. Они лишь поясняют, как можно прийти к этому уравнению. Доказательством правильности уравнения Шредингера является согласие с опытом тех выводов, к которым оно приводит.
Уравнение (217.1) является
обкщим уравнением Шредингера. Его также
называют уравнением Шреднягера,
зависящим от времени. Для многих
физических явлений, происходящих в
микромире, уравнение (217.1) можно упростить,
исключив зависимость
от времени, иными словами, найти уравнение
Шредингера для
стационарных
состояний
-
состояний с
фиксированными значениями энергии.
Это возможно,
если силовое поле, в котором частица
движется, стационарно, т. е. функция
![]() не зависит явно от времени и имеет смысл
потенциальной энергии. В данном случае
решение уравнения Шредингера может
быть представлено в виде произведения
двух функций, одна из которых есть
функция только координат, другая -
только времени, причем зависимость от
времени выражается множителем
не зависит явно от времени и имеет смысл
потенциальной энергии. В данном случае
решение уравнения Шредингера может
быть представлено в виде произведения
двух функций, одна из которых есть
функция только координат, другая -
только времени, причем зависимость от
времени выражается множителем
![]() так что
так что
где Е - полная энергия частицы, постоянная в случае стационарного поля. Подставляя (217.4) в (217.1), получим
откуда после деления на общий множительи соответствующих преобразований
придем к уравнению, определяющему функцию
 (217.5)
(217.5)
Уравнение (217.5) называется уравнением Шредингера для стационарных состояний. В это уравнение в качестве параметра входит полная энергия Е частицы. В теории дифференциальных уравнений доказывается, что подобные уравнения имеют бесчисленное множество решений, из которых посредством наложения граничных условий отбирают решения, имеющие физический смысл. Для уравнения Шредингера такими условиями являются условия регулярности волновых функций: волновые функции должны быть конечными, однозначными и непрерывными вместе со своими первыми производными. Таким образом, реальный физический смысл имеют только такие решения, которые выражаются регулярными функциямиНо регулярные решения имеют место не при любых значениях параметра Е, а лишь при определенном их наборе, характерном для данной задачи. Эти значения энергии называются собствев-нымн. Решения же, которые соответствуют собственным значениям энергии, называются собственными функциями. Собственные значения Е могут образовывать как непре-
рывный, так и дискретный ряд. В первом случае говорят о непрерывном, или сплошном, спектре, во втором - о дискретном спектре.
§ 218. Принцип причинности ■ квантовой механике
Из соотношения неопределенностей часто делают вывод о неприменимости принципа причинности к явлениям, происходящим в микромире. При этом основываются на следующих соображениях. В классической механике, согласно принципу причинности - принципу классического детермизма, по известному состоянию системы в некоторый момент времени (полностью определяется значениями координат и импульсов всех частиц системы) и силам, приложенным к ней, можно абсолютно точно задать ее состояние в любой последующий момент. Следовательно, классическая физика основывается на следующем понимании причинности: состояние механической системы в начальный момент времени с известным законом взаимодействия частиц есть причина, а ее состояние в последующий момент - следствие.
С другой стороны, микрообъекты не могут иметь одновременно и определенную координату, и определенную соответствующую проекцию импульса (задаются соотношением неопределенностей (215.1)), поэтому и делается вывод о том, что в начальный момент времени состояние системы точно не определяется. Если же состояние системы не определено в начальный момент времени, то не могут быть предсказаны и последующие состояния, т. е. нарушается принцип причинности.
Однако никакого нарушения принципа причинности применительно к микрообъектам не наблюдается, поскольку в квантовой механике понятие состояния микрообъекта приобретает совершенно иной смысл, чем в классической механике. В квантовой механике состояние микрообъекта полностью определяется волновой функцией (х,у, z , t ), квадрат модуля которой(х,у, z , t )\ 2 задает плотность вероятности нахождения частицы в точке с координатами х, у, z .
В свою очередь, волновая функция(х,у, z , t ) удовлетворяет уравнению Шредин-гера (217.1), содержащему первую производную функции по времени. Это же означает, что задание функции(для момента времениt 0) определяет ее значение в последующие моменты. Следовательно, в квантовой механике начальное состояние
Есть причина, а состояниев последующий момент - следствие. Это и есть форма принципа причинности в квантовой механике, т. е. задание функциипредопределяет ее значения для любых последующих моментов. Таким образом, состояние системы микрочастиц, определенное в квантовой механике, однозначно вытекает из предшествующего состояния, как того требует принцип причинности.
Движение микрочастиц в различных силовых полях описывается в рамках нерелятивистской квантовой механики с помощью уравнения Шредингера, из которого вытекают наблюдаемые на опыте волновые свойства частиц. Это уравнение, как и все основные уравнения физики, не выводятся, а постулируется. Его правильность подтверждается согласием результатов расчета с опытом. Волновое уравнение Шредингера имеет следующий общий вид :
- (ħ 2 / 2m) ∙ ∆ψ + U (x, y, z, t) ∙ ψ = i ∙ ħ ∙ (∂ψ / ∂t)
где ħ = h / 2π, h = 6,623∙10 -34 Дж ∙ с - постоянная Планка;
m - масса частицы;
∆ - оператор Лапласа (∆ = ∂ 2 / ∂x 2 + ∂ 2 / ∂y 2 + ∂ 2 / ∂z 2);
ψ = ψ (x, y, z, t) - искомая волновая функция;
U (x, y, z, t) - потенциальная функция частицы в силовом поле, где она движется;
i - мнимая единица.
Это уравнение имеет решение лишь при условиях, накладываемых на волновую функцию:
- ψ (x, y, z, t) должна быть конечной, однозначной и непрерывной;
- первые производные от нее должны быть непрерывны;
- функция | ψ | 2 должна быть интегрируема, что в простейших случаях сводится к условию нормировки вероятностей.
∆ψ + (2m / ħ 2) ∙ (E - U) ∙ ψ = 0
где ψ = ψ (x, y, z) - волновая функция только координат;
E - параметр уравнения - полная энергия частицы.
Для этого уравнения реальный физический смысл имеют лишь такие решения, которые выражаются регулярными функциями ψ (называемыми собственными функциями), имеющими место только при определенных значениях параметра E, называемого собственным значением энергии. Эти значения E могут образовывать как непрерывный, так и дискретный ряд, т.е. как сплошной, так и дискретный спектр энергий.
Для какой-либо микрочастицы при наличии уравнения Шредингера типа (8.2) задача квантовой механики сводится к решению этого уравнения, т.е. нахождению значений волновых функций ψ = ψ (x, y, z), соответствующих спектру собственных энергией E. Далее находится плотность вероятности | ψ | 2 , определяющая в квантовой механике вероятность нахождения частицы в единичном объеме в окрестности точки с координатами (x, y, z).
Одним из простейших случаев решения уравнения Шредингера является задача о поведении частицы в одномерной прямоугольной "потенциальной яме" с бесконечно высокими "стенками". Такая "яма" для частицы, движущейся только вдоль оси Х, описывается потенциальной энергией вида
где l - ширина "ямы", а энергия отсчитывается от ее дна (рис. 8.1).
Уравнение Шредингера для стационарных состояний в случае одномерной задачи запишется в виде:
∂ 2 ψ / ∂x 2 + (2m / ħ 2) ∙ (E - U) ∙ ψ = 0

В силу того, что "стенки ямы" бесконечно высокие, частица не проникает за пределы "ямы". Это приводит к граничным условиям:
ψ (0) = ψ (l) = 0
В пределах "ямы" (0 ≤ x ≤ l) уравнение (8.4) сводится к виду:
∂ 2 ψ / ∂x 2 + (2m / ħ 2) ∙ E ∙ ψ = 0
∂ 2 ψ / ∂x 2 + (k 2 ∙ ψ) = 0
где k 2 = (2m ∙ E) / ħ 2
Решение уравнения (8.7) с учетом граничных условий (8.5) имеет в простейшем случае вид:
ψ (x) = A ∙ sin (kx)
где k = (n ∙ π)/ l
при целочисленных значениях n.
Из выражений (8.8) и (8.10) следует, что
E n = (n 2 ∙ π 2 ∙ ħ 2) / (2m ∙ l 2) (n = 1, 2, 3 ...)
т.е. энергия стационарных состояний зависит от целого числа n (называемого квантовым числом) и имеет определенные дискретные значения, называемые уровнями энергии.
Следовательно, микрочастица в "потенциальной яме" с бесконечно высокими "стенками" может находится только на определенном энергетическом уровне E n , т.е. в дискретных квантовых состояниях n.
Подставив выражение (8.10) в (8.9) найдем собственные функции
ψ n (x) = A ∙ sin (nπ / l) ∙ x
Постоянная интегрирования А найдется из квантовомеханического (вероятностного) условия нормировки

которое для данного случая запишется в виде:

Откуда в результате интегрирования получим А = √ (2 / l) и тогда имеем
ψ n (x) = (√ (2 / l)) ∙ sin (nπ / l) ∙ x (n = 1, 2, 3 ...)
Графики функции ψ n (х) не имеют физического смысла, тогда как графики функции | ψ n | 2 показывают распределение плотности вероятности обнаружения частицы на различных расстояниях от "стенок ямы"(рис. 8.1). Как раз эти графики (как и ψ n (х) - для сравнения) изучаются в данной работе и наглядно показывают, что представления о траекториях частицы в квантовой механике несостоятельны.
Из выражения (8.11) вытекает, что энергетический интервал между двумя соседними уровнями равен
∆E n = E n-1 - E n = (π 2 ∙ ħ 2) / (2m ∙ l 2) ∙ (2n + 1)
Отсюда видно, что для микрочастиц (типа электрона) при больших размерах "ямы" (l≈ 10 -1 м), энергетические уровни располагаются настолько тесно, что образуют практически непрерывный спектр. Такое состояние имеет место, например, для свободных электронов в металле. Если же размеры "ямы" соизмеримы с атомными (l ≈ 10 -10 м), то получается дискретный спектр энергии (линейчатый спектр). Эти виды спектров также могут быть изучены в данной работе для различных микрочастиц.
Другим случаем поведения микрочастиц (как, впрочем, и микросистем - маятников), часто встречаемым на практике (и рассматриваемым в этой работе), является задача о линейном гармоническом осцилляторе в квантовой механике.
Как известно, потенциальная энергия одномерного гармонического осциллятора массой m равна
U (x) = (m ∙ ω 0 2 ∙ x 2)/ 2
где ω 0 - собственная частота колебаний осциллятора ω 0 = √ (k / m);
k - коэффициент упругости осциллятора.
Зависимость (8.17) имеет вид параболы, т.е. "потенциальная яма" в данном случае является параболической (рис. 8.2).

Квантовый гармонический осциллятор описывается уравнением Шредингера (8.2), учитывающим выражение (8.17) для потенциальной энергии. Решение этого уравнения записывается в виде :
ψ n (x) = (N n ∙ e -αx2 / 2) ∙ H n (x)
где N n - постоянный нормирующий множитель, зависящий от целого числа n;
α = (m ∙ ω 0) / ħ;
H n (x) - полином степени n, коэффициенты которого вычисляются при помощи рекуррентной формулы при различных целочисленных n.
В теории дифференциальных уравнений можно доказать, что уравнение Шредингера имеет решение (8.18) лишь для собственных значений энергии:
E n = (n + (1 / 2)) ∙ ħ ∙ ω 0
где n = 0, 1, 2, 3... - квантовое число.
Это значит, что энергия квантового осциллятора может принимать лишь дискретные значения, т.е. квантуется. При n = 0 имеет место E 0 = (ħ ∙ ω 0) / 2, т.е. энергия нулевых колебаний, что является типичным для квантовых систем и представляет собой прямое следствие соотношения неопределенности.
Как показывает детальное решение уравнения Шредингера для квантового осциллятора , каждому собственному значению энергии при разных n соответствует своя волновая функция, т.к. от n зависит постоянный нормирующий множитель

а также H n (x) - полином Чебышева-Эрмита степени n.
При том первые два полинома равны:
H 0 (x) = 1;
H 1 (x) = 2x ∙ √ α
Любой последующий полином связан с нми по следующей рекуррентной формуле:
H n+1 (x) = 2x ∙ √ α ∙ H n (x) - 2n ∙ H n-1 (x)
Собственные функции типа (8.18) позволяют найти для квантового осциллятора плотность вероятности нахождения микрочастицы как | ψ n (х) | 2 и исследовать ее поведение на различных уровнях энергии. Решение этой задачи затруднительно ввиду необходимости использования рекуррентной формулы. Эта задача успешно может решаться лишь с использованием ЭВМ, что и делается в настоящей работе.
Из статистического толкования волн де Бройля (см. § и соотношения не- определенностей Гейзенберга (см. § 215) следовало, что уравнением движения в квантовой механике, описывающим движение микрочастиц в различных силовых полях, должно быть уравне- ние, из которого бы вытекали наблю- даемые на опыте волновые свойства частиц.
Основное уравнение должно быть уравнением относительно волновой функции так как именно она, или, точнее, величина |Ф|2, определяет вероятность пребывания частицы в мо- мент времени t в объеме dV, в обла- сти с координатами и х + dx, y+dy,
z и Так как искомое уравнениедолжно учитывать волновые свойства частиц, то оно должно быть волновым уравнением, подобно уравнению, опи- сывающему электромагнитные волны. Основное уравнение нерелятивист- ской квантовоймеханики сформулиро- вано в 1926 г. Э.Шредингером. Урав- нение Шредингера, как и все основные уравнения физики (например, уравне- ния Ньютона в классической механике и уравнения Максвелла для электро- магнитного поля), не выводится, а по- стулируется. Правильность этого урав- нения подтверждается согласием с опы- том получаемых с его помощью резуль- татов, что, в свою очередь, придает ему характер закона природы. Уравнение
 Шредингера имеет вид
Шредингера имеет вид
|
Мнимаяединица, y,z,t) -
Потенциальная функция частицы в си- ловом поле, в котором она движется; z,t) - искомая волновая функция
Уравнение справедливо для любой частицы (со спином, равным 0; см. § 225), движущейся с малой (по сравнению со скоростью света) скоро- стью, т. е. со скоростью v с. Оно до- полняется условиями, накладываемы- ми на волновую функцию: 1) волновая функция должна быть конечной, одно- значной и непрерывной (см. § 216);
2) производные -, -, --, долж-
дх ду
ны быть непрерывны; 3) функция |Ф|2 должна быть интегрируема; это усло- вие в простейших случаях сводится к
Условию нормировки (216.3).
Чтобы прийти к уравнению Шредингера, рассмотрим свободно движущуюся частицу, которой, согласно де Бройля, сопостав- ляется Для простоты рассмот- рим одномерный случай. Уравнение плоской волны, распространяющейся вдоль оси х, имеет вид (см. § 154) t) = A cos - илив комплекснойзаписи t)- Следовательно, плоская волна де Бройля имеет вид
![]() (217.2)
(217.2)
(учтено, что - = -). В квантово й
Показатель экспоненты берут со знаком « - », поскольку физический смысл имеет только |Ф|2, то это несуществен- но. Тогда
 |
Используя взаимосвязь между энерги- ей Е и импульсом = --) и подставляя
![]() выражения (217.3), получим дифференци- альное уравнение
выражения (217.3), получим дифференци- альное уравнение
которое совпадает с уравнением для случая U- О (мы рассматривали свободную частицу).
Если частица движется в силовом поле, характеризуемом потенциальной энерги- ей U, то полная энергия Е складывается из кинетической и потенциальной энергий. Проводя аналогичные рассуждения и ис- пользуя взаимосвязь между ("для
Случая = Е -U), придем к диффе- ренциальному уравнению, совпадающему с (217.1).
Приведенные рассуждения не долж- ны восприниматься как вывод уравне- ния Шредингера. Они лишь поясняют, как можно прийти к этому уравнению. Доказательством правильности уравне- ния Шредингера является согласие с опытом тех выводов, к которым приводит.
Уравнение (217.1) является общим уравнением Шредингера. Его также называют уравнением Шредингера, зависящим от времени. Для многих физических явлений, происходящих в микромире, уравнение (217.1) можно упростить, исключив зависимость времени, иными словами, найти урав- нение Шредингера для стационарных состояний - состояний с фиксирован- ными значениями энергии. Это возмож- но, если силовое поле, в котором час- тица движется, стационарно, т. е. функ- ция U= z) не зависит явно от вре- мени и имеет смысл потенциальной энергии.
В данном случае решение уравнения Шредингера может быть представлено в виде произведения двух функций, одна из которых есть функция только координат, другая - только времени, причем зависимость от времени выража-
Ется множителем е" = е, так что
![]() (217.4)
(217.4)
где Е - полная энергия частицы, посто- янная в случае стационарного поля. Подставляя (217.4) в (217.1), получим

Откуда после деления па общий множи- тель е соответствующих преобра-
 зовании придем к уравнению, опреде- ляющему функцию
зовании придем к уравнению, опреде- ляющему функцию
Уравнение урав-
нением Шредингера для стационар- ных состояний. В это уравнение в ка- честве параметра входит полная энер- гия Е частицы. В теории дифференци- альных уравнений доказывается, что подобные уравнения имеют бесчислен- ное множество решений, из которых по- средством наложения граничных усло- вий отбирают решения, имеющие фи- зический
Для уравнения Шредингера такими условиями являются условия регуляр- ности волновых функций: волновые функции должны быть конечными, од- нозначными и непрерывными вместе со своими первыми производными.
Таким образом, реальный физичес- кий смысл имеют только такие реше- ния, которые выражаются регулярны- ми функциями Но регулярные реше- ния имеют место не при любых значе- ниях параметра Е, а лишь при опреде- ленном их наборе, характерном для дан- ной задачи. Эти значения энергии на- зываются собственными. Решения же, которые соответствуют собственным значениям энергии, называются соб- ственными функциями. Собственные значения Е могут образовывать как не- прерывный, так и дискретный ряд. В пер- вом случае говорят о непрерывном, или сплошном, спектре, во втором - о дис- кретном спектре.
§ 218. Принцип причинности в квантовой механике
Из соотношения неопределенностей часто делают вывод о неприменимости
принципа причинности к явлениям, происходящим в микромире. При этом основываются на следующих соображе- ниях. В классической механике, соглас- но принципупричинности- принци- пу классического детерминизма, по известному состоянию системы в неко- торый момент времени (полностью оп- ределяется значениями координат и импульсов всех частиц системы) и си- лам, приложенным к ней, можно абсо- лютно точно задать ее состояние в лю- бой последующий момент. Следова- тельно, классическая физика основыва- ется на следующем понимании причин- ности: состояние механической систе- мы в начальный момент времени с из- вестным законом взаимодействия час- тиц есть причина, а ее состояние в пос- момент - следствие.
С другой стороны, микрообъекты не могут иметь одновременно и опреде- ленную координату, и определенную соответствующую проекцию импульса [задаются соотношением неопределен- ностей поэтому и делается вы- вод о том, что в начальный момент вре- мени состояние системы точно не оп- ределяется. Если же состояние системы не определенно в начальный момент времени, то не могут быть предсказаны и последующие состояния, т. е. наруша- ется принцип причинности.
Однако никакого нарушения прин- ципа причинности применительно к микрообъектам не наблюдается, по- скольку в квантовой механике понятие состояния микрообъекта приобретает совершенно иной смысл, чем в класси- ческой механике. В квантовой меха- нике состояние микрообъекта полнос- тью определяется волновой функцией квадрат модуля которой
2 задает плотность вероятно- сти нахождения частицы в точке с ко- ординатами х, у, z.
В свою очередь, волновая функция удовлетворяет уравнению
Шредингера содержащему пер- вую производную функции Ф по време- ни. Это же означает, что задание функ- ции (для момента времени опре- деляет ее значение в последующие мо- менты. Следовательно, в квантовой ме- ханике начальное состояние есть причина, а состояние Ф в последующий момент - следствие. Это и есть форма принципа причинности в квантовой механике, т.е. задание функции пре- допределяет ее значения для любых последующих моментов. Таким обра- зом, состояние системы микрочастиц, определенное в квантовой механике, однозначно вытекает из предшествую- щего состояния, как того требует прин- цип причинности.
§219. Движение свободной частицы
Свободнаячастица - частица,дви- жущаяся в отсутствие внешних полей. Так как на свободную (пусть она движется вдоль оси х) силы не дей- ствуют, то потенциальная энергия час- тицы U(x) = const и ее можно принять равной нулю. Тогда полная энергия ча- стицы совпадает с ее кинетической энергией. В таком случае уравнение Шредингера (217.5) для стационарных состояний примет вид
![]() (219.1)
(219.1)
Прямой подстановкой можно убе- диться в том, что частным решением уравнения (219.1) является функция - где А = const и к = const, с собственным значением энергии
Функция = = представляет собой только координат- ную часть волновой функции Поэтому зависящая от времени волно- вая функция, согласно (217.4),

(219.3) представляет собой плоскую монохроматическую волну де Бройля [см. (217.2)].
Из выражения (219.2) следует, что зависимость энергии от импульса
![]()
оказывается обычной для нерелятиви- стских частиц. Следовательно, энергия свободной частицы может принимать любые значения (так как волновое чис- ло к может принимать любые положи- тельные значения), т. е. энергетический спектр свободной частицы является непрерывным.
Таким образом, свободная квантовая частица описывается плоской монохро- матической волной де Бройля. Этому соответствует не зависящая от време- ни плотность вероятности обнаружения частицы в данной точке пространства
т. е. все положения свободной частицы в пространстве являются равновероят- ными.
§ 220. Частица в одномерной прямоугольной «потенциальной яме» с бесконечно высокими
«стенками»
Проведем качественный анализ ре- шений уравнения Шредингера приме-
 Рис. 299
Рис. 299
 (220.4)
(220.4)
нительно к частице в одномерной пря- моугольной «потенциальной яме» с бесконечно высокими «стенками». Та- кая «яма» описывается потенциальной энергией вида (для простоты принима- ем, что частица движется вдоль оси х)

где ширина «ямы», а энергия отсчи- тывается от ее дна (рис. 299).
Уравнение Шредингера (217.5) для стационарных состояний в случае одно- мерной задачи запишется в виде
![]()
![]() По условию задачи (бесконечно вы- сокие «стенки»), частица не проникает за пределы «ямы», поэтому вероятность ее обнаружения (а следовательно, и вол- новая функция) за пределами «ямы» равна нулю. На границах «ямы» (при х-
0 и х =
непрерывная волновая функция также должна обращаться в нуль. Следовательно, граничные усло- вия в данном случае имеют вид
По условию задачи (бесконечно вы- сокие «стенки»), частица не проникает за пределы «ямы», поэтому вероятность ее обнаружения (а следовательно, и вол- новая функция) за пределами «ямы» равна нулю. На границах «ямы» (при х-
0 и х =
непрерывная волновая функция также должна обращаться в нуль. Следовательно, граничные усло- вия в данном случае имеют вид
В пределах «ямы» (0 х урав- нение Шредингера (220.1) сведется к уравнению
| |
|||
Общее решение дифференциально- го уравнения (220.3):
Так как по (220.2) = 0, то В = 0.
![]() (220.5)
(220.5)
Условие (220.2) = 0 выполняется только при где п - целые числа, т. е. необходимо, чтобы
 Из выражений (220.4) и (220.6) сле- дует,
Из выражений (220.4) и (220.6) сле- дует,
т. е. стационарное уравнение Шредин- гера, описывающее движение частицы в «потенциальной яме» с бесконечно высокими «стенками», удовлетворяет- ся только при собственных значени- ях зависящих от целого числа п. Следовательно, энергия частицы в
«потенциальной яме» с бесконечно вы- сокими «стенками» принимает лишь определенныедискретныезначения, т.е. квантуется.
Квантованные значения энергии называются уровнями энергии, а чис- ло п, определяющее энергетические уровни частицы, называется главным квантовым числом. Таким образом, микрочастица в «потенциальной яме» с бесконечно высокими «стенками» может находиться только на определен- ном энергетическом уровне или, как говорят, частица находится в квантовом
Подставив в (220.5) значение к из (220.6), найдем собственные функции:
| |
Постоянную интегрирования А най- дем из условия нормировки (216.3), которое для данного случая запишется в виде

В результате интегрирования полу-
А - а собственные функции будут иметь вид

I рафики собственных функции (220.8), соответствующие уровням
энергии (220.7) при п=1,2, 3, приведе- ны на рис. 300, а. На рис. 300, б изобра- жена плотность вероятности обнаруже- ния частицы на различных расстояни- ях от «стенок» ямы, равная =
Для п= 1, 2 и 3. Из рисун- ка следует, что, например, в квантовом состоянии с п = 2 частица не может на- ходиться в середине «ямы», в то время как одинаково часто может пребывать в ее левой и правой частях. Такое пове- дение частицы указывает на то, что представления о траекториях частицы в квантовой механике несостоятельны. Из выражения (220.7) вытекает, что энергетический интервал между двумя
Соседними уровнями равен
 |
Например, для электрона при раз- мерах ямы - 10"1 м (свободные элек-

Троны в металле) 10 Дж
Т. е. энергетические уровни расположены столь тесно, что спектр практически можно считать непрерыв- ным. Если же размеры ямы соизмери- мы с атомными м), то для электрона Дж эВ, т.е. получаются явно дискретные зна- чения энергии (линейчатый спектр).
Таким образом, применение уравне- ния Шредингера к частице в «потенци- альной яме» с бесконечно высокими
«стенками» приводит к квантованным значениям энергии, в то время как клас- сическая механика на энергию этой ча- стицы никаких ограничений не накла- дывает.
Кроме того,
Рассмотрение данной задачи приводит к выводу, что частица «в потенциаль- ной яме» с бесконечно высокими «стен- ками» не может иметь энергию меньше
Минимальной, равной [см. (220.7)].
Наличие отличной от нуля мини- мальной энергии не случайно и выте- кает из соотношения неопределеннос- тей. Неопределенность координаты Ах частицы в «яме» шириной Ах= Тогда, согласно соотношению неопре- деленностей импульс не может иметь точное, в данном случае нулевое, значение. Неопределенность импульса
Такому разбросу значений
импульса соответствует кинетическая энергия
![]()
Все остальные уровни (п > 1) име- ют энергию, превышающую это мини- мальное значение.
Из формул (220.9) и (220.7) следу- ет, что при больших квантовых числах
т. е. соседние уровни расположены тес- но: тем теснее, чем больше п. Если п очень велико, то можно говорить о практически непрерывной последова- тельности уровней и характерная осо- бенность квантовых процессов - диск- ретность - сглаживается. Этот резуль- тат является частным случаем принци- па соответствия Бора (1923), соглас- но которому законы квантовой механи- ки должны при больших значениях квантовых чисел переходить в законы классической физики.
Более общая трактовка принципа соответствия: всякая новая, более общая теория, являющаяся развитием классической, не отвергает ее полнос- тью, а включает в себя классическую теорию, указывая границы ее примене- ния, причем в определенных предель- ных случаях новая теория переходит в старую. Так, формулы кинематики и динамики специальной теории относи- тельности переходят при v с в форму- лы механики Ньютона. Например, хотя гипотеза да Бройля приписывает вол- новые свойства всем телам, но в тех слу- чаях, когда мы имеем дело с макроско- пическими телами, их волновыми свой- ствами можно пренебречь, т.е. приме- нять классическую механику Ньютона.
§ 221. Прохождение частицы сквозь потенциальный барьер.
Туннельный эффект
 простейший потенци- альный барьер прямоугольной формы (рис. для одномерного (по оси движения частицы. Для потенциально- го барьера прямоугольной формы вы- сотой шириной /можем записать
простейший потенци- альный барьер прямоугольной формы (рис. для одномерного (по оси движения частицы. Для потенциально- го барьера прямоугольной формы вы- сотой шириной /можем записать
При данных условиях задачи клас- сическая частица, обладая энергией Е, либо беспрепятственно пройдет над ба- рьером (при Е > U), либо отразится от него (при Е < U) будет двигаться в обратную сторону, т.е. она не может проникнуть сквозь барьер. Для микро- частицы, даже при Е > U, имеется от- личная от нуля вероятность, что части- ца отразится от барьера и будет двигать- ся в обратную сторону. При Е име- ется также отличная от нуля вероят- ность, что частица окажется в области х> т.е. проникнет сквозь барьер. По- добные, казалось бы, парадоксальные выводы следуют непосредственно из решения уравнения Шредингера, опи-
 412
412
сывающего движение микрочастицы при условиях данной задачи.
 Уравнение (217.5) для стационарных состояний для каждой из выделенных рис. 301, а
области име- ет
Уравнение (217.5) для стационарных состояний для каждой из выделенных рис. 301, а
области име- ет
(для областей
(для области
Общие решения этих дифференци- альных уравнений:
Решение (221.3) содержит также волны (после умножения на временной множитель), распространяющиеся в обе стороны. Однако в области 3 име- ется только волна, прошедшая сквозь барьер и распространяющаяся слева направо. Поэтому коэффициент формуле (221.3) следует принять рав- ным нулю.
В области 2
решение зависит от со- отношений E>U
или Е
(для области
(для области 2);
Значение q и 0, полу- чим решения уравнения Шредингера для трех областей в следующем виде:
(для области 3).
В частности, для области 1 полная волновая функция, согласно (217.4), будет иметь вид
 |
В этом выражении первое слагаемое представляет собой плоскую волну типа (219.3), распространяющуюся в положительном направлении оси х (со- ответствует частице, движущейся в сто- рону барьера), а второе - волну, рас- пространяющуюся в противоположном направлении, т. е. отраженную от барь- ера (соответствует частице, движущей- ся от барьера налево).
(для области 3).
 В области 2
функция уже не соответствует плоским волнам, распро- страняющимся в обе стороны, посколь- ку показатели степени экспонент не мнимые, а действительные. Можно по- казать, что для частного случая высо- кого и широкого барьера, когда 1,
В области 2
функция уже не соответствует плоским волнам, распро- страняющимся в обе стороны, посколь- ку показатели степени экспонент не мнимые, а действительные. Можно по- казать, что для частного случая высо- кого и широкого барьера, когда 1,
Качественный характер функций и иллюстрируется на рис. 301, откуда следует, что волно-
Функция не равна нулю и внутри ба- рьера, а в области 3, если барьер не очень широк, будет опять иметь вид волн де Бройля с тем же импульсом, т. е. с той же частотой, но с меньшей ампли- тудой. Следовательно, получили, что частица имеет отличную от нуля веро- ятность прохождения сквозь потенци- альный барьер конечной ширины.
Таким образом, квантовая механика приводит к принципиально новому спе- цифическому квантовому явлению, по- лучившему название туннельного эф- фекта, в результате которого микро- объект может «пройти» сквозь потен- циальный барьер. через Совместное решение уравнений для прямоугольного потенциального барьера дает (в предпо- ложении, что коэффициент прозрачно- сти мал по сравнению с единицей)
где - постоянный множитель, кото- рый можно приравнять единице; U - высота потенциального барьера; Е - энергия частицы; - ширина барьера.
Из выражения (221.7) следует, что D сильно зависит от массы т частицы, ширины / барьера и от (U - чем шире барьер, тем меньше вероятность прохождения сквозь него частицы.
Для потенциального барьера произ- вольной формы (рис. 302), удовлетво- ряющей условиям так называемого ква- зиклассического приближения (доста- точно гладкая форма кривой), имеем
| |
где U= U(x).
С классической точки зрения про- хождение частицы сквозь потенциаль- ный барьер при Е невозможно, так как частица, находясь в области барье- ра, должна была бы обладать отрица- тельной кинетической энергией. Тун- нельный эффект является специфиче- ским квантовым эффектом.
Прохождение частицы сквозь об- ласть, в которую, согласно законам клас- сической механики, она не может про- никнуть, можно пояснить соотношени- ем неопределенностей. Неопределен- ность импульса Ар на отрезке Ах = со- ставляет Ар > -. Связанная с этим раз- бросом в значениях импульса кинети-
 302
302
Ческая энергия может оказаться
достаточной для того, чтобы полная
энергия частицы оказалась больше по- тенциальной.
Основы теории туннельных перехо- дов заложены в работах Л. И. Мандель- штама
Туннельное прохождение сквозь потен- циальный барьер лежит в основе мно- гих явлений физики твердого тела (на- пример, явления в контактном слое на границе двух полупроводников), атом- ной и ядерной физики (например, распад, протекание термоядерных реак- ций).
§ 222. Линейный гармонический осциллятор
В квантовой механике
Линейный гармонический осцил- лятор - система, совершающая одно- мерное движение под действием квази- упругой силы, - является моделью, ис- пользуемой во многих задачах класси- ческой и квантовой теории (см. § 142). Пружинный, физический и математи- ческий маятники - примеры класси- ческих гармонических осцилляторов.
Потенциальная энергия гармони- ческого осциллятора [см. (141.5)] равна
Где - собственная частота колебаний осциллятора; т - масса частицы.
Зависимость (222.1) имеет вид пара- болы (рис. 303), т.е. «потенциальная яма» в данном случае является парабо- лической.
Амплитуда малых колебаний клас- сического осциллятора определяется его полной энергией Е (см. рис. 17).
дингера учитывающим выраже- ние (222.1) для потенциальной энергии. Тогда стационарные состояния кванто- вого осциллятора определяются урав- нением Шредингера вида
![]() = 0, (222.2)
= 0, (222.2)
где Е - полная энергия осциллятора. В теории дифференциальных урав-
нений доказывается, что уравнение (222.2) решается только при собствен- ных значениях энергии
![]() (222.3)
(222.3)
Формула (222.3) показывает, что энергия квантового осциллятора может
иметь лишь дискретные значения, т. е. квантуется. Энергия ограничена сни- зу отличным от нуля, как и для прямо- угольной «ямы» с бесконечно высоки- ми «стенками» (см. § 220), минималь- ным значением энергии = Су-
ществование минимальной энергии - она называется энергией нулевых ко- лебаний - является типичной для кван- товых систем и представляет собой пря- мое следствие соотношения неопреде- ленностей.
Наличие нулевых колебаний означа- ет, что частица не может находиться на дне «потенциальной ямы» (независимо от формы ямы). В самом деле, «падение на дно ямы» связано с обращением в нуль импульса частицы, а вместе с тем и его неопределенности. Тогда неопреде- ленность координаты становится сколь угодно большой, что противоречит, в свою очередь, пребыванию частицы в
«потенциальной яме».
Вывод о наличии энергии нулевых колебаний квантового осциллятора про- тиворечит выводам классической тео- рии, согласно которой наименьшая энергия, которую может иметь осцил- лятор, равна нулю (соответствует поко- ящейся в положении равновесия части- це). Например, согласно выводам клас- сической физики при Т = 0 энергия колебательного движения атомов кри- сталла должна была бы обращаться в нуль. Следовательно, должно исчезать и рассеяние света, обусловленное коле- баниями атомов. Однако эксперимент показывает, что интенсивность рассея- ния света при понижении температуры не равна нулю, а стремится к некоторо- му предельному значению, указываю- щему на то, что при Т 0 колебания атомов в кристалле не прекращаются. Это является подтверждением наличия нулевых колебаний.

Из формулы (222.3) также следует, что уровни энергии линейного гармо- нического осциллятора расположены на одинаковых расстояниях друг от друга (см. рис. 303), а именно расстоя- ние между соседними энергетическими уровнями равно причем минималь- ное значение энергии =
Строгое решение задачи о квантовом осцилляторе приводит еще к одному значительному отличию от классиче
Обще уравнение Шредингера. Уравнение Шредингера для стационарных состояний
Статистическое толкование волн де Бройля (см. § 216) и соотношение неопределенностей Гейзенберга (см. 5 215) привели к выводу, что уравнением движения в квантовой механике, описывающим движение микрочастиц в различных силовых полях, должно быть уравнение, из которого бы вытекали наблюдаемые на опыте волновые свойства частиц. Основное уравнение должно быть уравнением относительно волновой функции Ψ (х, у, z, t), так как именно она, или, точнее, величина |Ψ| 2 , определяет вероятность пребывания частицы в момент времени t в объеме dV, т. е. в области с координатами x и x+dx, y иy+dy, z и z+dz. Так как искомое уравнение должно учитывать волновые свойства частиц, то оно должно быть волновым уравнением, подобно уравнению, описывающему электромагнитные волны.
Основное уравнение нерелятивистской квантовой механики сформулировано в 1926 г. Э. Шредингером. Уравнение Шредингера,как и все основные уравнения физики (например, уравнения Ньютона в классической механике и уравнения Максвелла для электромагнитного поля), не выводится, а постулируется. Правильность этого уравнения подтверждается согласием с опытом получаемых с его помощью результатов, что, в свою очередь, придает ему характер закона природы. Уравнение Шредингера имеет вид
где h=h/(2π), m-масса частицы, ∆ -оператор Лапласа ( ),
),
i - мнимая единица, U (х, у, z, t) - потенциальная функция частицы в силовом поле, в котором она движется, Ψ (х, у, z, t) - искомая волновая функция частицы.
Уравнение (217.1) справедливо для любой частицы (со спином, равным 0; см. § 225), движущейся с малой (по сравнению со скоростью света) скоростью, т. е. со скоростью υ<<с. Оно дополняется условиями, накладываемыми на волновую функцию: 1) волновая функция должна быть конечной, однозначной и непрерывной (см. § 216); 2) производные

должны быть непрерывны; 3) функция |Ψ| 2 должна быть интегрируема; это условие в простейших случаях сводится к условию нормировки вероятностей (216.3).
Чтобы прийти к уравнению Шредингера, рассмотрим свободно движущуюся частицу, которой, согласно идее де Бройля, сопоставляется плоская волна. Для простоты рассмотрим одномерный случай. Уравнение плоской волны, распространяющейся вдоль оси х, имеет вид (см. § 154)
Или в комплексной записи ![]() . Следовательно, плоская волна де Бройля имеет вид
. Следовательно, плоская волна де Бройля имеет вид
![]() (217.2)
(217.2)
(учтено, что ω = E/h, k=p/h). В квантовой механике показатель экспоненты берут со знаком минус, но поскольку физический смысл имеет только |Ψ| 2 , то это (см. (217.2)) несущественно. Тогда
 ,
,
 ; (217.3)
; (217.3)
Используя взаимосвязь между энергией Е и импульсом p (E = p 2 /(2m)) и подставляя выражения (217.3), получим дифференциальное уравнение

которое совпадает с уравнением (217.1) для случая U= 0 (ми рассматривали свободную частицу).
Если частица движется в силовом поле, характеризуемом потенциальной энергией U, то полная энергия Е складывается из кинетической и потенциальной энергий. Проводя аналогичные рассуждения используя взаимосвязь между Еи р (для данного случая р 2 /(2m)=E -U), прядем к дифференциальному уравнению, совпадающему с (217.1).
Приведенные рассуждения не должны восприниматься как вывод уравнения Шредингера. Они лишь поясняют, как можно прийти к этому уравнению. Доказательством правильности уравнения Шредингера является согласие с опытом тех выводов, к которым оно приводит.
Уравнение (217.1) является общим уравнением Шредингера. Его также называют уравнением Шредингера, зависящем от времени. Для многих физических явлений, происходящих в микромире, уравнение (217.1) можно упростить, исключив зависимость Ψ от времени, иными словами, найти уравнение Шредингера для стационарных состоянии - состоянии с фиксированными значениями энергии. Это возможно, если силовое поле, в котором частица движется, стационарно, т. е. функция U = U(х, у, z) не зависит явно от времени и имеет смысл потенциальной энергии. В данном случае решение уравнения Шредингера может быть представлено в виде произведения двух функций, одна из которых есть функция только координат, другая - только времени, причем зависимость от времени выражается множителем
![]() ,
,
где Е - полная энергия частицы, постоянная в случае стационарного поля. Подставляя (217.4) в (217.1), получим
откуда после деления на общий множитель е – i (E/ h) t и соответствующих преобразований придем к уравнению, определяющему функцию ψ:
![]() (217.5)
(217.5)
Уравнение (217.5) называетсяуравнением Шредингера для стационарных состояний.
В это уравнение в качестве параметра входит полная энергия Е частицы. В теории дифференциальных уравнений доказывается, что подобные уравнения имеют бесчисленное множество решений, из которых посредством наложения граничных условий отбирают решения, имеющие физический смысл. Для уравнения Шредингера такими условиями являются условия регулярности волновых функций: волновые функции должны быть конечными, однозначными и непрерывными вместе со своими первыми производными. Таким образом, реальный физический смысл имеют только такие решения, которые выражаются регулярными функциями ψ. Но регулярные решения имеют место не при любых значениях параметра Е, а лишь при определенном их наборе, характерном для данной задачи. Эти значения энергии называютсясобственными. Решения же, которые соответствуютсобственным значениям энергии, называютсясобственными функциями. Собственные значения Е могут образовывать как непрерывный, так и дискретный ряд. В первом случае говорят о непрерывном, или сплошном, спектре, во втором - о дискретном спектре.

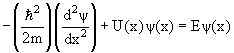 или
или


