Метод ромберга интегрирование. Решение дифференциальных уравнений. Смотреть что такое "ромберга метод" в других словарях

Пусть требуется вычислить определенный интеграл на интервале .

Далеко не всегда задача может быть решена аналитически. В частности, численное решение требуется в том случае, когда подынтегральная функция задана таблично. Для численного интегрирования подынтегральную функцию аппроксимируют какой-либо более простой функцией, интеграл от которой может быть вычислен. Обычно в качестве аппроксимирующей функции используют полином. В случае полинома нулевой степени метод численного интегрирования называют методом прямоугольников , в случае полинома первой степени – методом трапеций , в случае полинома второй степени – методом Симпсона . Все эти методы являются частными случаями квадратурных формул Ньютона-Котеса .

Итак, в методе трапеций подынтегральную функцию аппроксимируют полиномом первой степени, то есть прямой линией. Это значит, что вместо площади криволинейной трапеции мы будем искать площадь прямоугольной трапеции. Приближенное значение интеграла равно

Погрешность этой формулы равна .

Обозначим , где . Смысл введенного обозначения станет ясен несколько позже.

Оценку значения интеграла можно сделать более точной, если разбить интервал на n частей и применить формулу трапеций для каждого такого интервала

Если разбить интервал на две части, то есть уменьшит шаг в два раза , то оценка для величины интеграла будет иметь вид

В данном случае суммирование включает только один элемент. Обратите внимание, в новую оценку вошла старая оценка. Нам потребовалось определять значение функции только в новых узлах.

Если имеется 2 n подынтервалов, то

Если n=0, то

Если n=1, то

Если n=2, то

Вообще, справедливо рекуррентное соотношение

Полученное соотношение называют рекурсивной формулой трапеций и часто применяют для вычисления определенных интегралов. Преимущество этой формулы состоит в том, что при увеличении числа подынтервалов функцию нужно вычислять только во вновь добавленных точках. К сожалению, с помощью этой формулы нельзя получить сколь угодно точное значение интеграла. Во-первых, при увеличении числа разбиений объем вычислений стремительно возрастает; во-вторых, на каждом шаге накапливается ошибка округлений. Для дальнейшего уточнения значения интеграла можно сделать следующий шаг – экстраполировать полученную последовательность значений на случай бесконечного числа точек или что то же самое, на случай нулевого шага. Такой подход называется методом Ромберга .

Метод Ромберга заключается в том, что полученные оценки значения интеграла экстраполируют на случай бесконечного числа разбиений (величины шага равной нулю) по рекуррентной формуле

То есть строится следующий треугольник

R (2,1) R (2,2)

R (3,1) R (3,2) R (3,3)

R (4,1) R (4,2) R (4,3) R (4,4)

R (5,1) R (5,2) R (5,3) R (5,4) R (5,5) ,

в котором первый столбец состоит из значений интеграла, полученных при последовательном удвоении числа интервалов. Второй столбец – результат уточнения значений первого столбца по рекуррентной формуле. Третий столбец – уточненные значения интеграла на основе второго столбца и т.д. .

РОМБЕРГА МЕТОД

п р а в и л о Р о м б е р г а,- метод вычисления определенного интеграла, основанный на Ричардсона экстраполяции. Пусть вычисляется значение I нек-рого функционала, при этом вычисляемое приближенное значение Т(h)зависит от параметра h, так что в результате вычисления получается приближенное равенство . Пусть известна о поведении разности I - Т(h). как функции от h, а именно:

где т - натуральное число и a зависит от приближаемого функционала и той функции, на к-рой он вычисляется, от способа приближения и (слабо) от h. Если наряду с Т(h)вычислено Т(2h),то способ Ричардсона дает для Iприближение

(2)

Узлами квадратурной суммы являются точки

А ее коэффициенты - положительные числа. Квадратурная (5) точна для всех многочленов степени не выше 2l+1.

В предположении, что подинтегральная f(x)имеет непрерывную производную порядка 2l+ 2на , разность имеет представление вида (1), в к-ром т= 2l+ 2. Отсюда следует, что элементы (l+2)-гo столбца, вычисляемые по формуле (4), являются улучшениями по Ричардсону элементов (l+l)-гo столбца. В частности, для погрешности квадратурной формулы трапеций справедливо представление

и способ Ричардсона дает более точное приближение к I:

Оказывается квадратурной суммой формулы Симпсона, и т. к. для погрешности этой формулы справедливо представление

то снова можно воспользоваться способом Ричардсона и т. д.

В Р. м. в качестве приближения к I берется Т 0п , при этом предполагается, что существует непрерывная f (2n) (х)на . Ориентировочное представление о точности приближения Т 0п можно получить, сравнивая T 0n и T 1 , n _ 1 .

Впервые метод изложен В. Ромбергом .

Лит. :[l] R o m b e r g W., "Kgl. norske vid. selskabs forhandl.", 1955, Bd 28, № 7, s. 30-36; В a u e r F. L., R u t i s h a u s e r H., Stief1 E, "Proq. Symp. Appl. Math.", 1963, v. 15, p. 199-218. И. П. Мысовских .

Математическая энциклопедия. - М.: Советская энциклопедия . И. М. Виноградов . 1977-1985 .

Смотреть что такое "РОМБЕРГА МЕТОД" в других словарях:

Метод ускорения сходимости решений разностных задач (см. Аппроксимация дифференциальной краевой задачи разностной). Основная идея метода состоит в исследовании решения и h,(x) сходящейся разностной задачи при фиксированных хкак функции параметра… … Математическая энциклопедия

TABES DORSALIS - (спинная сухотка, сухотка спинного мозга, прогрессивная локомоторная атаксия, ataxie locomotrice progressive), хрон. сифилитическое заболевание нервной системы, поражающее преимущественно в спинном мозгу систему задних столбов и задних корешков,… …

I Обследование больного Обследование больного комплекс исследований, направленных на выявление индивидуальных особенностей больного, установление диагноза болезни, обоснование рационального лечения, определение прогноза. Объем исследований при О … Медицинская энциклопедия

ВЕСТИБУЛЯРНЫЕ МЕТОДЫ ИССЛЕДОВАНИЯ - ВЕСТИБУЛЯРНЫЕ МЕТОДЫ ИССЛЕДОВАНИЯ, состоят в а) подробном опросе б ного в отношении его жалоб и субъективных ощущений, относящихся к статическому аппарату, и б) в объективном испытании В. аппарата. Это испытание делится на 1) исследование… … Большая медицинская энциклопедия

СИФИЛИС - СИФИЛИС. Содержание: I. История сифилиса...............515 II. Эпидемиология.................519 III. Социальное значение сифилиса........524 IV. Spirochaeta pallida ............., 527 V. Патологическая анатомия...........533 VІ.… … Большая медицинская энциклопедия

ДВИЖЕНИЯ - ДВИЖЕНИЯ. Содержание: Геометрия Д....................452 Кинематика Д...................456 Динамика Д....................461 Двигательные механизмы............465 Методы изучения Д. человека.........471 Патология Д. человека............. 474… … Большая медицинская энциклопедия

МОЗЖЕЧКОВО-МОСТОВОЙ УГОЛ - (Klein hirnbruckenwinkel, angle ponto cerebelleuse, по нек рым angle ponto bulbo cerebelleuse) занимает своеобразное место в невропатологии, неврогистопатологии и неврохирургии. Названием этим обозначается угол между мозжечком, продолговатым… … Большая медицинская энциклопедия

МЕТОДЫ ВРАЧЕБНОГО ИССЛЕДОВАНИЯ - І. Общие принципы врачебного исследования. Рост и углубление наших знаний, все большее, и большее техническое оснащение клиники, основанное на использовании новейших достижений физики, химии и техники, связанное с этим усложнение методов… … Большая медицинская энциклопедия

- (США) (United States of America, USA). I. Общие сведения США государство в Северной Америке. Площадь 9,4 млн. км2. Население 216 млн. чел. (1976, оценка). Столица г. Вашингтон. В административном отношении территория США … Большая советская энциклопедия

Проходил с 9 декабря 1946 по 20 августа 1947 года. Этот процесс был первым в череде двенадцати последующих Нюрнбергских процессов . Официально он назывался «США против Карла Брандта» и проходил в восточном флигеле дворца правосудия Нюрнберга.… … Википедия

Задача численного интегрирования состоит в замене исходной подинтегральной функции f(x), для которой трудно или невозможно записать первообразную в аналитике, некоторой аппроксимирующей функцией φ(x) . Такой функцией обычно является полином (кусочный полином) . То есть:
,
где – априорная погрешность метода на интервале интегрирования,
а r(x) – априорная погрешность метода на отдельном шаге интегрирования.

Обзор методов интегрирования.

Методы вычисления однократных интегралов называются квадратурными (для кратных интегралов – кубатурными ).

Метод прямоугольников.

Различают метод левых, правых и средних прямоугольников. Суть метода ясна из рисунка. На каждом шаге интегрирования функция аппроксимируется полиномом нулевой степени – отрезком, параллельным оси абсцисс.

Выведем формулу метода прямоугольников из анализа разложения функции f(x) в ряд Тейлора вблизи некоторой точки x = x i .

Рассмотрим диапазон интегрирования от x i до x i +h , где h – шаг интегрирования.

Вычислим …=

= = . Получили формулу правых (или левых) прямоугольников и априорную оценку погрешности r на отдельном шаге интегрирования. Основной критерий, по которому судят о точности алгоритма – степень при величине шага в формуле априорной оценки погрешности.

В случае равного шага h на всем диапазоне интегрирования общая формула имеет вид

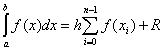Здесь n – число разбиений интервала интегрирования, . Для справедливости существования этой оценки необходимо существование непрерывной f"(x).

Метод средних прямоугольников . Здесь на каждом интервале значение функции считается в точке , то есть . Разложение функции в ряд Тейлора показывает, что в случае средних прямоугольников точность метода существенно выше:

Метод трапеций.

Аппроксимация в этом методе осуществляется полиномом первой степени. Суть метода ясна из рисунка.

На единичном интервале
.
В случае равномерной сетки (h = const)

При этом , а 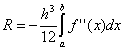. Погрешность метода трапеций в два раза выше, чем у метода средних прямоугольников! Однако на практике найти среднее значение на элементарном интервале можно только у функций, заданных аналитически (а не таблично), поэтому использовать метод средних прямоугольников удается далеко не всегда. В силу разных знаков погрешности в формулах трапеций и средних прямоугольников истинное значение интеграла обычно лежит между двумя этими оценками.

Особенности поведения погрешности.

Казалось бы, зачем анализировать разные методы интегрирования, если мы можем достичь высокой точности, просто уменьшая величину шага интегрирования. Однако рассмотрим график поведения апостериорной погрешности R результатов численного расчета в зависимости от числа n разбиений интервала (то есть при шаг . На участке (1) погрешность уменьшается в связи с уменьшением шага h. Но на участке (2) начинает доминировать вычислительная погрешность, накапливающаяся в результате многочисленных арифметических действий. Таким образом, для каждого метода существует своя R min , которая зависит от многих факторов, но прежде всего от априорного значения погрешности метода R .

Уточняющая формула Ромберга.

Метод Ромберга заключается в последовательном уточнении значения интеграла при кратном увеличении числа разбиений. В качестве базовой может быть взята формула трапеций с равномерным шагом h .
Обозначим интеграл с числом разбиений n = 1 как .
Уменьшив шаг в два раза, получим .
Если последовательно уменьшать шаг в 2 n раз, получим рекуррентное соотношение для расчета .

Пусть мы вычислили четыре раза интеграл с n от 1 до 4. Представим следующий треугольник:
R(1;1)
R(2;1) R(2;2)
R(3;1) R(3;2) R(3;3)
R(4;1) R(4;2) R(4;3) R(4;4)

В первом столбце стоят значения интеграла, полученные при последовательном удвоении числа интервалов. Следующие столбцы – результаты уточнения значения интеграла по следующей рекуррентной формуле:

Правое нижнее значение в треугольнике – искомое уточненное значение интеграла.

Метод Симпсона.

Подынтегральная функция f(x) заменяется интерполяционным полиномом второй степени P(x) – параболой, проходящей через три узла, например, как показано на рисунке ((1) – функция, (2) – полином).

Рассмотрим два шага интегрирования (h = const = x i+1 – x i ), то есть три узла x 0 , x 1 , x 2 , через которые проведем параболу, воспользовавшись уравнением Ньютона:
.
Пусть z = x - x 0 ,
тогда

Теперь, воспользовавшись полученным соотношением, сосчитаем интеграл по данному интервалу:

.

При вычислении одной и той же величины формулы с большим числом узлов дают более высокий порядок точности, но они более громоздки. Для оценки их точности надо привлекать дополнительный узел, что требует еще более сложных вычислений. Рассмотрим более простой способ получения высокого порядка точности.

Из формулы (12) видно, что погрешность простейшей формулы (7) для четырежды дифференцируемой функции имеет вид , где - некоторая точка вблизи узла Если липшиц-непрерывна, то оценку нетрудно уточнить:

Пусть в общем случае имеется некоторая приближенная формула для вычисления величины по значениям на равномерной сетке с шагом h, а остаточный член этой формулы имеет следующую структуру:

Произведем теперь расчет по той же приближенной формуле для той же точки но используя равномерную сетку с другим шагом Тогда получим значение связанное с точным значением соотношением

Заметим, что Имея два расчета на разных сетках, нетрудно оценить величину погрешности. Для этого вычтем (13) из (14) и получим первую формулу Рунге:

Первое слагаемое справа есть главный член погрешности. Таким образом, расчет по второй сетке позволяет оценить погрешность расчета на первой сетке (с точностью до членов более высокого порядка).

Можно исключить найденную погрешность (15) из формулы (13) и получить результат с более высокой точностью по второй формуле Рунге:

Этот метод оценки погрешности и повышения точности результата очень прост, применим в большом числе случаев и исключительно эффективен. Рассмотрим два примера его применения к численному дифференцированию.

Таблица 7

Пример 1. Пусть функция задана таблицей 7 и требуется вычислить Выберем для вычислений простейшую формулу (6). Полагая , т. е. производя вычисления по точкам получим . Увеличивая шаг вдвое , т. е. вычисляя производную по точкам получим . Проводя вычисления по формуле Рунге (16), где согласно оценке (6) берется получим уточненное значение ; это всего 2% отличается от искомого значения .

Пример 2. Выведем формулу высокой точности из формулы низкой точности.

Возьмем простейшую формулу для вычисления первой производной в середине интервала (8) и запишем ее, выбирая сначала соседние узлы, а затем более удаленные:

Порядок точности формулы , а коэффициент увеличения шага , поэтому уточнение методом Рунге дает формулу (9):

Отсюда видно, что для получения высокого порядка точности не обязательно производить вычисления непосредственно по формулам высокого порядка точности; можно произвести вычисления по простым формулам низкой точности на разных сетках и затем уточнить результат методом Рунге. Последний способ предпочтительней еще потому, что величина поправки (15) дает апостериорную оценку точности.

Метод Рунге обобщается на случай произвольного числа . Пусть функция имеет достаточно высокие непрерывные производные. Тогда в разложениях Тейлора типа (11) можно удерживать большое число членов и подстановка их в формулы типа приводит к представлению остаточного члена в виде ряда

Пусть расчет проведен на q различных сетках с шагами . Тогда из остаточного члена можно исключить первые слагаемых. Для этого перепишем соотношение (17), оставляя первые члены погрешности:

Это система линейных уравнений относительно величии Решая ее по правилу Крамера, получим уточненное значение по формуле Ромберга

Эта формула приводит к повышению порядка точности результата на по сравнению с исходной формулой , т. е. каждая лишняя сетка позволяет повысить порядок точности на единицу.

Формула Ромберга удобна тем, что ее можно применять при любом числе равномерных сеток и любом соотношении их шагов. Ее недостатками являются сравнительная громоздкость и отсутствие в промежуточных выкладках апостериорных оценок точности. Если сетки выбраны так, что сгущение сеток происходит всегда в одно и то же число раз (т. е. ), то вместо формулы Ромберга удобнее рекуррентно применять метод Рунге.

Для этого берут последовательные пары сеток и т. д. По каждой паре производят уточнение методом Рунге, исключая тем самым главный член погрешности . Поэтому в уточненных величинах главный член погрешности будет иметь вид , где шаг можно условно принять для первой пары сеток за для второй - за и т. д. (это верно, только если одинаково для всех пар сеток). Уточненные значения таким же образом группируют в пары и исключают ошибку следующего порядка Всего можно произвести уточнение, на единицу меньше числа сеток. При каждом уточнении вычисляется погрешность (15), дающая апостериорную оценку точности на данном этапе вычислений. Пример такого вычисления будет дан в главе IV.

Замечание 1. Если исходная формула для вычисления имеет симметричный вид, то на равномерной сетке обычно все нечетные члены ряда (17) обращаются в нуль. При этом пользоваться общей формулой (18) можно, но невыгодно, ибо она не учитывает дополнительной информации о нулевых коэффициентах. Следует оставить в сумме (17) только степени и соответственно изменить формулу Ромберга. Аналогично изменяется рекуррентная процедура Рунге: при очередном исключении ошибки порядок точности повышается не на 1, а на 2. Примером может служить данный выше вывод формулы (9) из формулы (8), когда после первого уточнения погрешность уменьшилась с сразу до

Замечание 2. Допустимое число членов суммы (17) связано с количеством существующих у функции непрерывных производных. Поэтому для недостаточно гладких функций бессмысленно брать большое число сеток. Практически даже для «хороших» функций используют не более 3 - 5 сеток; обычно отношение их шагов стараются выбрать равным 2.

Замечание 3. Метод Рунге-Ромберга можно применять только в том случае, если ошибка представима в виде (17), где коэффициенты одинаковы для всех сеток. Строго говоря, при численном дифференцировании эти коэффициенты зависят от положения узлов сетки.

Но если выбранные конфигурации узлов на всех сетках подобны относительно точки (рис. 14, а), то зависимость от узлов одинакова для всех сеток и сводится к величине шага. Тогда метод Рунге - Ромберга применим. Если же правило подобия нарушено (рис. 14, б, в), то метод применять нельзя.

Поэтому при численном дифференцировании метод Рунге-Ромберга удается применять только для нахождения производных в узлах или серединах интервалов равномерных (или описанных далее квазиравномерных) сеток. Но эти случаи являются достаточно важными в практических приложениях. Особенно широко применяется описанный метод при численном интегрировании и разностных методах решения задач для дифференциальных и интегральных уравнений.

ЖУРНАЛ ВЫЧИСЛИТЕЛЬНОЙ МАТЕМАТИКИ И МАТЕМАТИЧЕСКОЙ ФИЗИКИ, 2009, том 49, < 2, с. 232-240

УДК 519.644.7

ПРИМЕНЕНИЕ МЕТОДА РОМБЕРГА ДЛЯ ПОВЫШЕНИЯ ТОЧНОСТИ ВЫЧИСЛЕНИЯ КРАТНЫХ ИНТЕГРАЛОВ

(141980 Дубна, ОИЯИ)

e-mail: [email protected]

Поступила в редакцию 24.05.2007 г. Переработанный вариант 03.03.2008 г.

Известный метод Ромберга, применяемый для повышения точности вычисления одномерных интегралов, обобщен на случай кратных интегралов, если для их вычисления используется произведение составных квадратурных формул. При определенных условиях коэффициенты формулы Ромберга оказываются независимыми от кратности интеграла, что позволяет использовать простой алгоритм вычислений, развитый для одномерных интегралов. Даются примеры расчетов по методу Ромберга для интегралов кратности от двух до шести и производится сравнение с некоторыми другими методами. Библ. 9. Табл. 3.

Ключевые слова: численное интегрирование, кратные интегралы, метод Ромберга.

1. ВВЕДЕНИЕ

Метод Ромберга хорошо известен как техника, позволяющая повышать точность вычислений одномерных интегралов путем составления определенной линейной комбинации их значений, полученных на разных сетках интегрирования . В многомерном случае получение подобных наборов приближенных значений затруднительно, если они вычисляются путем последовательного применения какой-либо квадратурной формулы.

Пусть функция/(х1, ..., хр) определена на множестве О = {а1 < х1 < Ь1, ..., ар < хр < Ьр}. Будем вычислять интеграл

?) = / //(Х1.....Хр) йХ1... йХр (1)

с помощью формулы

/) = Ъ... Ър В>1... 0]р/(а 1 + ]1НЪ..., ар + ]рНр), (2)

>1 =0 ]р = 0

которая является произведением составных квадратурных формул с постоянными шагами интегрирования Ък:

Sk(Ik) = hk ^ DjkIk(xlf..., xkak + jkhk), (3)

к = 1, 2, ..., р. Здесь Мк - число разбиений отрезка интегрирования [ак, Ьк], Ък = (Ьк - ак)/Мк, В> -коэффициенты формулы (3),

(x1, , xk) - J -"J f(x1, > xp) dxk +1 ■■■dxp,

1р(х1, ..., xp) = /(x1, ..., xp). Погрешность формулы (2) R(/) = I(f) - £(f) можно представить в виде (СМ. )

R = Е0 + Й1 £ ^ ^ + Й1Й2 £ 2 ЕI,2 +

>1 = 0 ,1=0 ,2 = 0

Й!...йр2... 2 1 _1,

>1 = 0 -1 = 0

где Ек. 1 - погрешность формулы (3).

Пусть для интегрирования по всем переменным хь..., хр используется одна и та же квадратурная формула ЗД) с погрешностью Е = 0(Икт). Обозначим через М общее число областей разбиения исходной области О. Если И1 = ... = Ир = И, тогда М = N и суммарная погрешность R оценивается как R = 0(М~т/р). С ростом кратности р увеличение N ведет к все более значительному росту объема вычислений. В этом случае с относительно небольшими вычислительными затратами бывает возможно получить только несколько приближенных значений интеграла, соответствующих небольшим значениям N. Такие аппроксимации обычно являются слишком грубыми, однако их линейная комбинация по методу Ромберга, который фактически означает увеличение т (см. ), может оказаться удовлетворительной по точности. Таким образом, при некоторых р и определенном выборе сеток интегрирования такой подход может оказаться эффективным по соотношению вычислительных затрат и точности получаемых результатов.

В данной статье метод Ромберга применен для случая, когда интегрирование по всем переменным выполняется по формуле трапеций.

2. МЕТОД ВЫЧИСЛЕНИИ Рассмотрим составную формулу трапеций:

1к) = Йк 2 ^}к1к(Х1" " Хк-1, ак + >кЙк),

Г 1, если ]к = 1, 2, ..., Ик -1 >к = 11/2, если ]к = 0, Ик,

к = 1, 2, ..., р. В одномерном случае в предположении конечности (21 + 2)-й производной подынтегральной функции /(х) погрешность формулы (5) можно представить в форме (см. )

Rtr(/) = - 2 72тй2т(/(2т-;)(Ь) -/(2т-;)(а)) + г(й),

где а, Ь - пределы интегрирования,

г (й) = -у 21 + 2/(21 + 2)(^)й2" + 2(ь - а), а Ь.

Числа У; удовлетворяют равенству

Ниже приводятся значения некоторых из них:

У 2 = 1 1 " У 4 = ТОП" У 6 = алоил" У 8 = 1опплпп" У10 =

12 14 720 16 30240 18 1209600 110 47900160"

Следовательно, если функции 1к(х1, ..., хк), к = 1, 2, ..., р, имеют ограниченные частные производные (1к(х;, хк)) 2тпорядка 21 + 2, погрешность формулы (5) можно записать в виде

Е"-1(4) = 2 Стк(1к)(Йк)2т + Гк(Йк) ,

&тк(1к) = -У 2 [(1к (X;,. > Хк - 1» Ьк)) 2т-1 - (1к(X;, Хк-1, ак)) 2т-1 ],

Гк(Йк) = -У 21 + 2 (1к(х1,; Хк-;Лк)) 21 + 2(Йк)21 +2 (Ьк - ак) .

ак < < Ьк. Подставляя это выражение при к = 1, 2, ..., р в формулу (4), получаем

R = 2 °т;(I;)(Й;)2 т + г; (й;) +

Й1 2 2 Ст2(12)(Й2)2т + Г2(Й2)

Й; .Йр-1 2- 2 ^р-1 2 °тр(1р)(Йр) 2 т + Гр (ЙР)

>1 = 0 -1 = 0

Введем обозначения

Втк(1к) = Й1 Йк-1 2- 2 - ВЬСтк(1к) .

>1 = 0 -1 = 0

Вт1 (4)= ^т1 (11) , к = 1 2,., р.

Тогда выражение для R можно записать в виде

R = 2 Вт;(I;)(Й;)2т + г;(Й;) +

2 Вт2(12)(Й2)2т + Й; 2 ^Г2(Й2) + ...

2 Втр(1 р)(йр) т+й1-йр-; 2- 2 выгР(й?) =

>1 = 0 }р-1 = 0

22 Втк(1к)(Йк)2т + R*,

R * = Г; (Й;) + Й; 2 ^ Г2 (Й2) + ... + Й; - Йр _; 2- 2 ^ ;Гр (Йр). >1=0 >1 = 0 -1 = 0 Предположим теперь, что интеграл (1) вычисляется I + 1 раз по формуле (2) при

Ир = Ир, X Ир,...Д ^,

где X - некоторая положительная постоянная.

Введем индекс г для обозначения номера соответствующего вычисления интеграла при N1, ..., Мр. Все величины, зависящие от Мк, также будут иметь индекс г. Тогда числа разбиения N1 и шаги сетки интегрирования Н"к можно выразить через степени X следующим образом:

Мк = Ък = X"Л°, к = 1, 2, ..., р, г = 0, 1, I.

Имеем равенства

1(/) = й(/) + /) = й(/) + XX г(1к)(Ък)2т + Л*,

г = 0, 1, ..., I. Образуем линейную комбинацию этих соотношений с некоторыми коэффициентами сг, потребовав, чтобы выполнялось условие

1(/) = X сй; (/) + X X X сВтк I (4)(Ък)2т + X сЛ *.

0 к=1т= 1 г = 0 I = 0

Для коэффициентов Вткг(1к) выполняются неравенства:

\Вткг(4)|< л1 ... Лк_ 1 X- X В>к-11 Отк(1к)|<

< Ртк(1к)П(Ь«-ап) ^ -1- X- X Вк-l,

N1 Nk-1 >1 = 0 >к-1 = 0

Ртк(4) = тах |^тк(4)| , к = 1, 2, ..., р, т = 1, 2,-, /.

X ... X В...=1,

"1 "k- 1 >1 = 0 Л-1 = 0

к = 2, 3, ..., р, г = 0, 1, ..., I. Следовательно,

\Втк г (4)|< ртк(1к)П(Ьп-ап) для к = 2, 3, ..., р, т = 1, 2, ..., I,

Вткг (11)|< Рт1(4) длЯ I = 0, 1, ..., I.

Тогда с учетом (6) имеем

I (/)-X (/)-X с л

< X Рт1(11)(Ъ0)

XX ртк(4)П(Ьп-ап)()

Потребуем теперь, чтобы выполнялись условия

2СX "" = 0, т =1, 2, ..., I.

Эти условия совместно с условием (7) образуют систему из I + 1 линейно независимых уравнений, из которой определяются I + 1 неизвестных коэффициентов с. Подставив эти коэффициенты в неравенство (9), получим

I (/) = 2 С&(/) + RRomb, (10)

^отЬ = 2 С; = 0

R* = г;(й1)+Й1 2 Г2(Й2) + -+Й1 -йр-; 2- 2 - ^Гр(йр),

>1 = 0 >1 = 0 }р-1 = 0

Гк(йк) = -У21 + 2(1к(Х;, ..., Хк-1,^к)) 21 + 2(йк)21 + 2(Ьк - ак).

Теорема. Пусть функция /(х1, ..., хр) имеет ограниченные частные производные / 21+2 (х1, ..., хр),

к = 1, 2, ..., р. Тогда погрешность формулы (10) удовлетворяет неравенству

|^оть| <| У 21 + 2 Рг П(Ь" - а")2 таХ /Х2" + 2 (Х1" Хр)|(Й0)21 +2, (11)

А А О I хк I

Рг = 2 С Х-2"1 +!).

Доказательство. Согласно свойствам определенных интегралов и свойствам интегрирования по параметру имеем

(1к(x1, - , Хк)) 2г + 2= -ТГГ2 I -I /(х;, - , хр)Лхк + 1- ЛХр =

1 -1/Х2 + 2(Х1" -" Хр+ 1 - Лхр,

тах |(4(X;, -, Хк)) 21+2 = тах

1 -1/ч +2(X1, -, XP)^к +1 -

<тах|/г2г+2(X;,-, Xp)| П (Ьп - ап), к = 1,-, р - 1.

Для к = р имеем Ь^, ..., X,) = /(x1, ..., xp) и

тах |(1р(X;, -, Xp))^ = таХ/x2г + 2(X;, -, Xp)| .

X,-, xp\ лр I О I

Тогда для величины т* = тах \тк\ справедливо неравенство

т*(Ък) < |у21 + 2таХ/х21+2(Х1, Хр)|П(Ьп - ап)(Ък)2" + 2, к = 1, 2,., р.

I + 2Г""Л|.У Т2" + 2

С учетом (8) получим

\Я*\ < т*(Л1) + (Ь - а1)т*(Л2) + ... + (Ь1-а1)...(Ьр-1-ар-1)т*(лр) =

IУ 21 +2 П(Ьп - ап)X таХ /Х2" + 2 (Х1, Хр)|(Ък)

А А О I Хк I

^ мп = XI срп <

<|У21 + 2 П(Ьп - ап)XтаХ+2(Хl, ХрIX 1с""1(Ък)

Используя соотношение (6), из этого неравенства получаем оценку (11).

3. ПРОГРАММНАЯ РЕАЛИЗАЦИЯ

Следует заметить, что коэффициенты сг формулы (10) не зависят от кратности вычисляемых интегралов, поскольку сетки интегрирования (6) по всем переменным х1, ..., Хр образуются с использованием одного и того же значения постоянной X. Это позволяет применить в многомерном случае известный алгоритм, развитый для вычисления одномерных интегралов. Для X = 2 этот алгоритм определяется рекуррентной формулой :

^ = ^-1) + ($-1) - ^-1))/(22(>-1)-1).

Здесь £(1), г = 0, 1, ..., I, - значения интеграла (1), полученные с помощью составной формулы

трапеций (5) с соответствующими шагами интегрирования Ъ"к, к = 1, 2, ..., р. Величины Б(2), ...,

Б ■" + 1) представляют собой значения, уточненные с помощью формулы (10). Процедуру получения уточненных оценок по формуле (12) можно представить в виде следующей диаграммы (см. ):

С(1) с(1) с(1) с(1) Б0 Б1 Б2

На этой основе была написана компьютерная программа, по которой вычисление интеграла производится до тех пор, пока не выполнится одно из условий

тт|1 - 1 -1)<еаь8,

Величина £abs или erel задается пользователем. Результатом считается значение S-" +

Для дальнейшего прочтения статьи необходимо приобрести полный текст . Статьи высылаются в формате PDF на указанную при оплате почту. Время доставки составляет менее 10 минут . Стоимость одной статьи — 150 рублей .

Пoхожие научные работыпо теме «Математика»

ИНТЕГРИРОВАНИЕ ОСЦИЛЛИРУЮЩИХ ФУНКЦИЙ В КВАЗИТРЕХМЕРНОЙ ЗАДАЧЕ ЭЛЕКТРОДИНАМИКИ
ОСЕЛЕДЕЦ И.В., СТАВЦЕВ С.Л., ТЫРТЫШНИКОВ Е.Е. - 2009 г.
МОДИФИКАЦИЯ КВАДРАТУРНОЙ ФОРМУЛЫ ЭЙЛЕРА ДЛЯ ФУНКЦИЙ С ПОГРАНСЛОЙНОЙ СОСТАВЛЯЮЩЕЙ
ЗАДОРИН А.И. - 2014 г.