Система имеет единственное решение. Линейные уравнения. Решение систем линейных уравнений матричным методом. Методы решения систем линейных уравнений

Система линейных уравнений - это объединение из n линейных уравнений, каждое из которых содержит k переменных. Записывается это так:

Многие, впервые сталкиваясь с высшей алгеброй, ошибочно полагают, что число уравнений обязательно должно совпадать с числом переменных. В школьной алгебре так обычно и бывает, однако для высшей алгебры это, вообще говоря, неверно.

Решение системы уравнений - это последовательность чисел (k 1 , k 2 , ..., k n ), которая является решением каждого уравнения системы, т.е. при подстановке в это уравнение вместо переменных x 1 , x 2 , ..., x n дает верное числовое равенство.

Соответственно, решить систему уравнений - значит найти множество всех ее решений или доказать, что это множество пусто. Поскольку число уравнений и число неизвестных может не совпадать, возможны три случая:

Система несовместна, т.е. множество всех решений пусто. Достаточно редкий случай, который легко обнаруживается независимо от того, каким методом решать систему.
Система совместна и определена, т.е. имеет ровно одно решение. Классический вариант, хорошо известный еще со школьной скамьи.
Система совместна и не определена, т.е. имеет бесконечно много решений. Это самый жесткий вариант. Недостаточно указать, что «система имеет бесконечное множество решений» - надо описать, как устроено это множество.

Переменная x i называется разрешенной, если она входит только в одно уравнение системы, причем с коэффициентом 1. Другими словами, в остальных уравнениях коэффициент при переменной x i должен быть равен нулю.

Если в каждом уравнении выбрать по одной разрешенной переменной, получим набор разрешенных переменных для всей системы уравнений. Сама система, записанная в таком виде, тоже будет называться разрешенной. Вообще говоря, одну и ту же исходную систему можно свести к разным разрешенным, однако сейчас нас это не волнует. Вот примеры разрешенных систем:

Обе системы являются разрешенными относительно переменных x 1 , x 3 и x 4 . Впрочем, с тем же успехом можно утверждать, что вторая система - разрешенная относительно x 1 , x 3 и x 5 . Достаточно переписать самое последнее уравнение в виде x 5 = x 4 .

Теперь рассмотрим более общий случай. Пусть всего у нас k переменных, из которых r являются разрешенными. Тогда возможны два случая:

Число разрешенных переменных r равно общему числу переменных k : r = k . Получаем систему из k уравнений, в которых r = k разрешенных переменных. Такая система является совместной и определенной, т.к. x 1 = b 1 , x 2 = b 2 , ..., x k = b k ;
Число разрешенных переменных r меньше общего числа переменных k : r < k . Остальные (k − r ) переменных называются свободными - они могут принимать любые значения, из которых легко вычисляются разрешенные переменные.

Так, в приведенных выше системах переменные x 2 , x 5 , x 6 (для первой системы) и x 2 , x 5 (для второй) являются свободными. Случай, когда есть свободные переменные, лучше сформулировать в виде теоремы:

Обратите внимание: это очень важный момент! В зависимости от того, как вы запишете итоговую систему, одна и та же переменная может быть как разрешенной, так и свободной. Большинство репетиторов по высшей математике рекомендуют выписывать переменные в лексикографическом порядке, т.е. по возрастанию индекса. Однако вы совершенно не обязаны следовать этому совету.

Теорема. Если в системе из n уравнений переменные x 1 , x 2 , ..., x r - разрешенные, а x r + 1 , x r + 2 , ..., x k - свободные, то:

Если задать значения свободным переменным (x r + 1 = t r + 1 , x r + 2 = t r + 2 , ..., x k = t k ), а затем найти значения x 1 , x 2 , ..., x r , получим одно из решений.

Если в двух решениях значения свободных переменных совпадают, то значения разрешенных переменных тоже совпадают, т.е. решения равны.

В чем смысл этой теоремы? Чтобы получить все решения разрешенной системы уравнений, достаточно выделить свободные переменные. Затем, присваивая свободным переменным разные значения, будем получать готовые решения. Вот и все - таким образом можно получить все решения системы. Других решений не существует.

Вывод: разрешенная система уравнений всегда совместна. Если число уравнений в разрешенной системе равно числу переменных, система будет определенной, если меньше - неопределенной.

И все бы хорошо, но возникает вопрос: как из исходной системы уравнений получить разрешенную? Для этого существует

Запишите систему линейных алгебраических уравнений в общем виде

Что называется решением СЛАУ?

Решением системы уравнений называется набор из n чисел,

При подстановке которой в систему каждое уравнение обращается в тождество.

Какая система называется совместной (несовместной)?

Система уравнений называется совместной, если она имеет хотя бы одно решение.

Система называется несовместной, если она не имеет решений.

Какая система называется определенной (неопределенной)?

Совместная система называется определенной, если она имеет единственное решение.

Совместная система называется неопределенной, если она имеет больше одного решения.

Матричная форма записи системы уравнений

Ранг системы векторов

Ранг системы векторов называется максимальное число линейно независимых векторов.

Ранг матрицы и способы его нахождения

Ранг матрицы - наивысший из порядков миноров этой матрицы, определитель которых отличен от нуля.

Первый метод –- метод окантовки - заключается в следующем:

Если все миноры 1-го порядка, т.е. элементы матрицы равны нулю, то r=0 .

Если хоть один из миноров 1-го порядка не равен нулю, а все миноры 2-го порядка равны нулю то r=1.

Если минор 2-го порядка отличен от нуля то исследуем миноры 3-го порядка. Таким образом находят минор k-го порядка и проверяют, не равны ли нулю миноры k+1-го порядка.

Если все миноры k+1-го порядка равны нулю, то ранг матрицы равен числу k. Такие миноры k+1-го порядка, как правило, находят путем "окантовки" минора k-го порядка.

Второй метод определения ранга матрицы заключается в применении элементарных преобразований матрицы при возведении ее к диагональному виду. Ранг такой матрицы равно числу отличных от нуля диагональных элементов.

Общее решение неоднородной системы линейных уравнений, его свойства.

Свойство 1. Сумма любого решения системы линейных уравнений и любого решения соответствующей однородной системы является решением системы линейных уравнений.

Свойство 2. Разность любых двух решений неоднородной системы линейных уравнений является решением соответствующей однородной системы.

Метод Гаусса решения СЛАУ

Последовательность:

1)составляется расширенная матрица системы уравнения

2)с помощью элементарных преобразований матрица приводится к ступенчатому виду

3)определяется ранг расширенной матрицы системы и ранг матрицы системы и устанавливается пакт совместимости или несовместимости системы

4)в случае совместимости записывается эквивалентная система уравнения

5)находится решение системы. Главные переменные выражаются через свободные

Теорема Кронекера-Капелли

Теоре́ма Кро́некера - Капе́лли - критерий совместности системы линейных алгебраических уравнений:

Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг её основной матрицы равен рангу её расширенной матрицы, причём система имеет единственное решение, если ранг равен числу неизвестных, и бесконечное множество решений, если ранг меньше числа неизвестных.

Для того чтобы линейная система являлась совместной, необходимо и достаточно, чтобы ранг расширенной матрицы этой системы был равен рангу её основной матрицы.

Когда система не имеет решения, когда имеет единственное решение, имеет множество решений?

Если число уравнений системы равно числу неизвестных переменных и определитель ее основной матрицы не равен нулю,значит Такие системы уравнений имеют единственное решение, причем в случае однородной системы все неизвестные переменные равны нулю.

Система линейных уравнений, имеющая хотя бы одно решение, называется совместной. В противном случае, т.е. если система не имеет решений, то она называется несовместной.

Системой m линейных уравнений с n неизвестными называется система вида

где a ij и b i (i =1,…,m ; b =1,…,n ) – некоторые известные числа, а x 1 ,…,x n – неизвестные. В обозначении коэффициентов a ij первый индекс i обозначает номер уравнения, а второй j – номер неизвестного, при котором стоит этот коэффициент.

Коэффициенты при неизвестных будем записывать в виде матрицы , которую назовём матрицей системы .

Числа, стоящие в правых частях уравнений, b 1 ,…,b m называются свободными членами.

Совокупность n чисел c 1 ,…,c n называется решением данной системы, если каждое уравнение системы обращается в равенство после подстановки в него чисел c 1 ,…,c n вместо соответствующих неизвестных x 1 ,…,x n .

Наша задача будет заключаться в нахождении решений системы. При этом могут возникнуть три ситуации:

Система линейных уравнений, имеющая хотя бы одно решение, называется совместной . В противном случае, т.е. если система не имеет решений, то она называется несовместной .

Рассмотрим способы нахождения решений системы.

МАТРИЧНЫЙ МЕТОД РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ

Матрицы дают возможность кратко записать систему линейных уравнений. Пусть дана система из 3-х уравнений с тремя неизвестными:

Рассмотрим матрицу системы и матрицы столбцы неизвестных и свободных членов

Найдем произведение

т.е. в результате произведения мы получаем левые части уравнений данной системы. Тогда пользуясь определением равенства матриц данную систему можно записать в виде

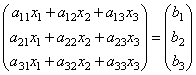или короче A ∙X=B .

Здесь матрицы A и B известны, а матрица X неизвестна. Её и нужно найти, т.к. её элементы являются решением данной системы. Это уравнение называют матричным уравнением .

Пусть определитель матрицы отличен от нуля |A | ≠ 0. Тогда матричное уравнение решается следующим образом. Умножим обе части уравнения слева на матрицу A -1 , обратную матрице A : . Поскольку A -1 A = E и E ∙X = X , то получаем решение матричного уравнения в виде X = A -1 B .

Заметим, что поскольку обратную матрицу можно найти только для квадратных матриц, то матричным методом можно решать только те системы, в которых число уравнений совпадает с числом неизвестных . Однако, матричная запись системы возможна и в случае, когда число уравнений не равно числу неизвестных, тогда матрица A не будет квадратной и поэтому нельзя найти решение системы в виде X = A -1 B .

Примеры. Решить системы уравнений.

ПРАВИЛО КРАМЕРА

Рассмотрим систему 3-х линейных уравнений с тремя неизвестными:

Определитель третьего порядка, соответствующий матрице системы, т.е. составленный из коэффициентов при неизвестных,

называется определителем системы .

Составим ещё три определителя следующим образом: заменим в определителе D последовательно 1, 2 и 3 столбцы столбцом свободных членов

Тогда можно доказать следующий результат.

Теорема (правило Крамера). Если определитель системы Δ ≠ 0, то рассматриваемая система имеет одно и только одно решение, причём

Доказательство . Итак, рассмотрим систему 3-х уравнений с тремя неизвестными. Умножим 1-ое уравнение системы на алгебраическое дополнение A 11 элемента a 11 , 2-ое уравнение – на A 21 и 3-е – на A 31 :

Сложим эти уравнения:

Рассмотрим каждую из скобок и правую часть этого уравнения. По теореме о разложении определителя по элементам 1-го столбца

Аналогично можно показать, что и .

Наконец несложно заметить, что

Таким образом, получаем равенство: .

Следовательно, .

Аналогично выводятся равенства и , откуда и следует утверждение теоремы.

Таким образом, заметим, что если определитель системы Δ ≠ 0, то система имеет единственное решение и обратно. Если же определитель системы равен нулю, то система либо имеет бесконечное множество решений, либо не имеет решений, т.е. несовместна.

Примеры. Решить систему уравнений

МЕТОД ГАУССА

Ранее рассмотренные методы можно применять при решении только тех систем, в которых число уравнений совпадает с числом неизвестных, причём определитель системы должен быть отличен от нуля. Метод Гаусса является более универсальным и пригоден для систем с любым числом уравнений. Он заключается в последовательном исключении неизвестных из уравнений системы.

Вновь рассмотрим систему из трёх уравнений с тремя неизвестными:

Первое уравнение оставим без изменения, а из 2-го и 3-го исключим слагаемые, содержащие x 1 . Для этого второе уравнение разделим на а 21 и умножим на –а 11 , а затем сложим с 1-ым уравнением. Аналогично третье уравнение разделим на а 31 и умножим на –а 11 , а затем сложим с первым. В результате исходная система примет вид:

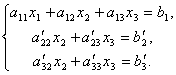
Теперь из последнего уравнения исключим слагаемое, содержащее x 2 . Для этого третье уравнение разделим на , умножим на и сложим со вторым. Тогда будем иметь систему уравнений:

Отсюда из последнего уравнения легко найти x 3 , затем из 2-го уравнения x 2 и, наконец, из 1-го – x 1 .

При использовании метода Гаусса уравнения при необходимости можно менять местами.

Часто вместо того, чтобы писать новую систему уравнений, ограничиваются тем, что выписывают расширенную матрицу системы:

и затем приводят её к треугольному или диагональному виду с помощью элементарных преобразований.

К элементарным преобразованиям матрицы относятся следующие преобразования:

перестановка строк или столбцов;
умножение строки на число, отличное от нуля;
прибавление к одной строке другие строки.

Примеры: Решить системы уравнений методом Гаусса.

Таким образом, система имеет бесконечное множество решений.

Система линейных алгебраических уравнений. Основные термины. Матричная форма записи.

Определение системы линейных алгебраических уравнений. Решение системы. Классификация систем.

Под системой линейных алгебраических уравнений (СЛАУ) подразумевают систему

Параметры aij называют коэффициентами , а bi – свободными членами СЛАУ. Иногда, чтобы подчеркнуть количество уравнений и неизвестных, говорят так «m×n система линейных уравнений», – тем самым указывая, что СЛАУ содержит m уравнений и n неизвестных.

Если все свободные члены bi=0 то СЛАУ называют однородной . Если среди свободных членов есть хотя бы один, отличный от нуля, СЛАУ называют неоднородной .

Решением СЛАУ (1) называют всякую упорядоченную совокупность чисел (α1,α2,…,αn), если элементы этой совокупности, подставленные в заданном порядке вместо неизвестных x1,x2,…,xn, обращают каждое уравнение СЛАУ в тождество.

Любая однородная СЛАУ имеет хотя бы одно решение: нулевое (в иной терминологии – тривиальное), т.е. x1=x2=…=xn=0.

Если СЛАУ (1) имеет хотя бы одно решение, ее называют совместной , если же решений нет – несовместной . Если совместная СЛАУ имеет ровно одно решение, её именуют определённой , если бесконечное множество решений – неопределённой .

Матричная форма записи систем линейных алгебраических уравнений.

С каждой СЛАУ можно связать несколько матриц; более того – саму СЛАУ можно записать в виде матричного уравнения. Для СЛАУ (1) рассмотрим такие матрицы:

Матрица A называется матрицей системы . Элементы данной матрицы представляют собой коэффициенты заданной СЛАУ.

Матрица A˜ называется расширенной матрицей системы . Её получают добавлением к матрице системы столбца, содержащего свободные члены b1,b2,...,bm. Обычно этот столбец отделяют вертикальной чертой, – для наглядности.

Матрица-столбец B называется матрицей свободных членов , а матрица-столбец X – матрицей неизвестных .

Используя введённые выше обозначения, СЛАУ (1) можно записать в форме матричного уравнения: A⋅X=B.

Примечание

Матрицы, связанные с системой, можно записать различными способами: всё зависит от порядка следования переменных и уравнений рассматриваемой СЛАУ. Но в любом случае порядок следования неизвестных в каждом уравнении заданной СЛАУ должен быть одинаков

Теорема Кронекера-Капелли. Исследование систем линейных уравнений на совместность.

Теорема Кронекера-Капелли

Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы системы, т.е. rangA=rangA˜.

Система называется совместной, если она имеет хоть одно решение. Теорема Кронекера-Капелли говорит вот о чём: если rangA=rangA˜, то решение есть; если rangA≠rangA˜, то данная СЛАУ не имеет решений (несовместна). Ответ на вопрос о количестве этих решений даёт следствие из теоремы Кронекера-Капелли. В формулировке следствия использована буква n, которая равна количеству переменных заданной СЛАУ.

Следствие из теоремы Кронекера-Капелли

Если rangA≠rangA˜, то СЛАУ несовместна (не имеет решений).

Если rangA=rangA˜

Если rangA=rangA˜=n, то СЛАУ является определённой (имеет ровно одно решение).

Заметьте, что сформулированная теорема и следствие из неё не указывают, как найти решение СЛАУ. С их помощью можно лишь выяснить, существуют эти решения нет, а если существуют – то сколько.

Методы решения СЛАУ

Метод Крамера

Метод Крамера предназначен для решения тех систем линейных алгебраических уравнений (СЛАУ), у которых определитель матрицы системы отличен от нуля. Естественно, при этом подразумевается, что матрица системы квадратна (понятие определителя существует только для квадратных матриц). Суть метода Крамера можно выразить в трёх пунктах:

Составить определитель матрицы системы (его называют также определителем системы), и убедиться, что он не равен нулю, т.е. Δ≠0.

Для каждой переменной xi необходимо составить определитель Δ X i , полученный из определителя Δ заменой i-го столбца столбцом свободных членов заданной СЛАУ.

Найти значения неизвестных по формуле xi= Δ X i /Δ

Решение систем линейных алгебраических уравнений с помощью обратной матрицы.

Решение систем линейных алгебраических уравнений (СЛАУ) с помощью обратной матрицы (иногда этот способ именуют ещё матричным методом или методом обратной матрицы) требует предварительного ознакомления с таким понятием как матричная форма записи СЛАУ. Метод обратной матрицы предназначен для решения тех систем линейных алгебраических уравнений, у которых определитель матрицы системы отличен от нуля. Естественно, при этом подразумевается, что матрица системы квадратна (понятие определителя существует только для квадратных матриц). Суть метода обратной матрицы можно выразить в трёх пунктах:

Записать три матрицы: матрицу системы A, матрицу неизвестных X, матрицу свободных членов B.

Найти обратную матрицу A -1 .

Используя равенство X=A -1 ⋅B получить решение заданной СЛАУ.

Метод Гаусса. Примеры решения систем линейных алгебраических уравнений методом Гаусса.

Метод Гаусса является одним из самых наглядных и простых способов решения систем линейных алгебраических уравнений (СЛАУ): как однородных, так и неоднородных. Коротко говоря, суть данного метода состоит в последовательном исключении неизвестных.

Преобразования, допустимые в методе Гаусса:

Смена мест двух строк;

Умножение всех элементов строки на некоторое число, не равное нулю.

Прибавление к элементам одной строки соответствующих элементов другой строки, умноженных на любой множитель.

Вычеркивание строки, все элементы которой равны нулю.

Вычеркивание повторяющихся строк.

Насчет последних двух пунктов: повторяющиеся строки можно вычёркивать на любом этапе решения методом Гаусса, – естественно, оставляя при этом одну из них. Например, если строки №2, №5, №6 повторяются, то можно оставить одну из них, – например, строку №5. При этом строки №2 и №6 будут удалены.

Нулевые строки убираются из расширенной матрицы системы по мере их появления.

Тема 2. Решение систем линейных алгебраических уравнений прямыми методами.

Системами линейных алгебраических уравнений (сокращенно - СЛАУ) называются системы уравнений вида

или, в матричном виде,

A × x = B , (2.2)

A - матрица коэффициентов системы размерности n ´ n

x - вектор неизвестных, состоящий из n компонент

B - вектор правых частей системы, состоящий из n компонент.

A = x = B = (2.3)

Решением СЛАУ является такой набор из n чисел, который будучи подставленным вместо значений x 1 , x 2 , … , x n в систему (2.1) обеспечивает равенство левых частей правым во всех уравнениях.

Каждая СЛАУ в зависимости от значений матриц A и B может иметь

Одно решение

Бесконечно много решений

Ни одного решения.

В данном курсе будем рассматривать только те СЛАУ, которые имеют единственное решение. Необходимым и достаточным условием этого является неравенство нулю определителя матрицы A .

Для поиска решений над системами линейных алгебраических уравнений могут проводиться некоторые преобразования, не изменяющие ее решений. Эквивалентными преобразованиями системы линейных уравнений называются такие ее преобразования, которые не изменяют ее решения. К их числу относятся:

Перестановка местами двух любых уравнений системы (следует отиетить, что в некоторых случаях, рассматриваемых ниже, это преробразование использовать нельзя);

Умножение (или деление) какого-либо уравнения системы на число, не равное нулю;

Прибавление к одному уравнению системы другого ее уравнения, умноженного (или разделенного) на некоторое не равное нулю число.

Методы решения СЛАУ делятся на две больших группы, называемые - прямые методы и итерационные методы . Имеется также способ сведения задачи решения СЛАУ к задаче поиска экстремума функции нескольких переменных с последующем решением ее методами поиска экстремума (об этом подробнее - при прохождении соответствующей темы). Прямые методы обеспечивают получение точного решения системы (если оно существует) за один шаг. Итерационные методы (если при этом обеспечена их сходимость) позволяют многократно улучшать некоторое начальное приближение к искомому решению СЛАУ и, вообще говоря, точного решения не дадут никогда. Однако, учитывая то, что прямые методы решения из-за неизбежных ошибок округления на промежуточных этапах расчетов тоже дают не идеально точные решения, итерационные методы могут тоже обеспечить примерно такой же результат.

Прямые методы решения СЛАУ. Наиболее часто используемыми прямыми методами решения СЛАУ являются:

Метод Крамера,

Метод Гаусса (и его модификация - метод Гаусса-Жордана)

Матричный метод (с использованием обращения матрицы A ).

Метод Крамера основан на вычислении определителя основной матрицы A и определителей матриц A 1 , A 2 , …, A n , которые получаются из матрицы A заменой в ней одного (i -го) столбца (i = 1, 2,…, n ) на столбец, содержащий элементы вектора B . После этого решения СЛАУ определяются как частное от деления значений этих определителей. Точнее, расчетные формулы имеют такой вид

(2.4)

Пример 1 . Найдем методом Крамера решение СЛАУ, у которой

A = , B = .

Имеем

A 1 = , A 2 = , A 3 = , A 4 = .

Вычислим значения определителей всех пяти матриц (c использованием функции МОПРЕД среды Excel ). Получим

Так как определитель матрицы A не равен нулю - система имеет единственное решение. Тогда определим его по формуле (2.4). Получим

Метод Гаусса. Решение СЛАУ этим методом предполагает составление расширенной матрицы системы A * . Расширенная матрица системы - это матрица размером в n строк и n +1 столбцов, включающая в себя исходную матрицу A c присоединенным к ней справа столбцом, содержащим вектор B .

A* = (2.4)

Здесь a in+1 =b i (i = 1, 2, …, n ).

Суть метода Гаусса состоит в приведении (посредством эквивалентных преобразований ) расширенной матрицы системы к треугольному виду (так, чтобы ниже ее главной диагонали находились только нулевые элементы).

A * =

Тогда, начиная с последней строки и двигаясь вверх, можно последовательно определить значения всех компонент решения.

Начало преобразований расширенной матрицы системы к необходимому виду заключается в просмотре значений коэффициентов при x 1 и выборе строки, в которой он имеет максимальное по абсолютной величине значение (это необходимо для уменьшения величины вычислительной ошибки при последующих вычислениях). Эту строку расширенной матрицы необходимо поменять местами с первой ее строкой (или же, что лучше, сложить (или вычесть) с первой строкой и результат поместить на место первой строки). После этого все элементы этой новой первой строки (в том числе и в последнем ее столбце) необходимо разделить на этот коэффициент. После этого вновь полученный коэффициент a 11 станет равным единице. Дальше от каждой из оставшихся строк матрицы необходимо вычесть ее первую строку, умноженную на значение коэффициента при x 1 в этой строке (т.е. на величину a i 1 , где i =2, 3, … n ). После этого во всех строках, начиная со второй коэффициенты при x 1 (т.е. все коэффициенты a i 1 (i =2, …, n ) будут равными нулю. Поскольку мы выполняли только эквивалентные преобразования - решение вновь полученной СЛАУ не будет отличаться от исходной системы.

Дальше, оставляя неизменной первую строку матрицы, проделаем все вышеописанные действия с остальными строками матрицы и, в результате, вновь полученный коэффициент a 22 станет равным единице, а все коэффициенты a i 2 (i =3, 4, …, n ) станут равными нулю. Продолжая аналогичные действия, мы в конечном итоге приведем нашу матрицу к виду, в котором все коэффициенты a ii = 1 (i =1, 2, …, n ), а все коэффициенты a ij = 0 (i =2, 3, …, n , j < i ). Если же на каком-то шаге при поиске наибольшего по абсолютной величине коэффициента при x j мы не сможем найти не равного нулю коэффициента - это будет значить, что исходная система не имеет единственного решения. В этом случае процесс решения необходимо прекратить.

Если процесс эквивалентных преобразований закончился успешно, то полученная в результате «треуголиная» расширенная матрица будет соответствовать такой системе линейных уравнений:

Из последнего уравнения этой системы найдем значение x n . Далее, подставляя это значение в предпоследнее уравнение, найдем значение x n -1 . После этого, подставляя оба эти найденных значения в третье снизу уравнение системы, найдем значение x n -2 . Продолжая так далее и продвигаясь по уравнением этой системы снизу вверх, будем последовательно находить значения других корней. И, наконец, подставляя найденные значения x n , x n -1 , x n -2 , x 3 и x 2 в первое уравнение системы найдем значение х 1 . Такая процедура поиска значений корней по найденной треугольной матрице называется обратным ходом. Процесс приведения исходной расширенной матрицы эквивалентными преобразованиями к треугольному виду назавают прямым ходом метода Гаусса..

Достаточно подробный алгоритм решения СЛАУ методом Гаусса приведен на рис. .2.1 и рис. 2.1а.

Пример 2 . Найти методом Гаусса решение той же СЛАУ, которую мы уже решали методом Крамера. Составим сначала ее расширенную матрицу. Получим

A * = .

Сначала переставим местами первую и третью строки этой матрицы (так как в ее первом столбце находится наибольший по абсолютной величине элемент), а затем разделим все элементы этой новой первой строки на значение 3. Получим

A * = .

A * =

Дальше переставим местами вторую и третью строки этой матрицы, разделим вторую строку переставленной матрицы на 2.3333 и, аналогично вышеописаному, обнулим коэффициенты во втором столбце третьей и четвертой строк матрицы. Получим

A * = .

После выполнения подобных действий над третьей и четвертой строками матрицы получим

A * = .

Разделив теперь четвертую строку на -5.3076, закончим проведение расширенной матрицы системы к диагональному виду. Получим

Рис. 2.1. Алгоритм решения систем линейных алгебраических уравнений методом Гаусса

Рис. 2.1а. Макроблок “Расчет значений решения”.

A * = .

Из последней строки сразу получим x 4 = 0.7536. Поднимаясь теперь вверх по строкам матрицы и выполняя расчеты, последовательно получим x 3 = 0.7971, x 2 =- 0.1015 и x 1 = 0.3333. Сравнивая полученное этим методом решение с решением, полученным методом Крамера, нетрудно убедиться в их совпадении.

Метод Гаусса-Жордана. Этот метод решения СЛАУ во многом похож на метод Гаусса. Основным отличием является то, что используя эквивалентные преобразования расширенная матрица системы уравнений приводится не к треугольному виду, а к диагональному виду, на главной диагонали которой находятся единицы, а вне нее (кроме последнего n +1 столбца) - нули. После окончания такого преобразования - последний столбец расширенной матрицы будет содержать решение исходной СЛАУ (т,е. . x i = a i n +1 (i = 1, 2, … , n ) в полученной матрице). Обратный ход (как в методе Гаусса) для окончательных расчетов значений компонент решения - не нужен.

Приведение матрицы к диагональному виду проводится, в основном, также как и в методе Гаусса. Если в строке i коэффициент при x i (i = 1, 2, … , n ) по абсолютной величине мал, то производится поиск строки j , в которой коэффициент при x i будет наибольшим по абсолютной величине эта (j -я) строка прибавляется поэлементно к i - й строке. Затем все элементы i - й строки делятся на значение элемента x i Но, в отличие от метода Гаусса, после этого идет вычитание из каждой строки с номером j строки с номером i ,умноженной на a ji , но условие j > i заменено на другоеВ методе Гаусса-Жордана идет вычитание из каждой строки с номером j , причем j # i , строки с номером i ,умноженной на a ji . Т.е. производится обнуление коэффициентов как ниже, так и выше главной диагонали.

Достаточно подробный алгоритм решения СЛАУ методом Гаусса–Жордана приведен на рис. 2.2.

Пример 3 . Найти методом Гаусса-Жордана решение той же СЛАУ, которую мы уже решали методами Крамера и Гаусса.

Полностью аналогично методу Гаусса составим расширенную матрицу системы. Затем переставим местами первую и третью строки этой матрицы (так как в ее первом столбце находится наибольший по абсолютной величине элемент), а затем разделим все элементы этой новой первой строки на значение 3. Дальше проведем вычитание из каждой строки матрицы (кроме первой) элементов первой строки, умноженных на коэффициент в первом столбце этой строки. Получим то же, что и в методе Гаусса

A * = .

Дальше переставим местами вторую и третью строки этой матрицы, разделим вторую строку переставленной матрицы на 2.3333 и (уже в отличие от метода Гаусса ) обнулим коэффициенты во втором столбце первой, третьей и четвертой строк матрицы. Получим